import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
Gradient Descent 2D
Interactive tutorial on gradient descent 2d with practical implementations and visualizations
sns.despine()<Figure size 432x288 with 0 Axes>init_x = 2
init_y = 5%matplotlib inlineimport numpy as np4.1*4.116.814.1-0.2*2*4.12.46x = 4.1
alpha = 0.2
iterations = 10
# for i in range(10):
for i in range(iterations):
x = x- (alpha*2*x)
print("(",round(x, 2),"," ,round(x*x, 2),")")( 2.46 , 6.05 )
( 1.48 , 2.18 )
( 0.89 , 0.78 )
( 0.53 , 0.28 )
( 0.32 , 0.1 )
( 0.19 , 0.04 )
( 0.11 , 0.01 )
( 0.07 , 0.0 )
( 0.04 , 0.0 )
( 0.02 , 0.0 )x = 4.1
alpha = 0.05
iterations = 20
# for i in range(10):
for i in range(iterations):
x = x- (alpha*2*x)
st = """
\begin{frame}{Iteration %d}
\begin{columns}
\begin{column}{0.6\textwidth}
\begin{adjustbox}{max totalsize={\textwidth},center}
\begin{tikzpicture}
\begin{axis}[
xlabel=$x$,
ylabel=$y$,
xmin=-4.2,
xmax=4.2,
axis x line*=bottom,
axis y line*=left,
xtick align=outside,
ytick align=outside,
legend pos=outer north east
]
\addplot[mark=none, gray] {x^2};\addlegendentry{$y=x^2$}
\addplot[only marks, mark=*]
coordinates{ % plot 1 data set
(%s,%s)
};
\end{axis}
\end{tikzpicture}
\end{adjustbox}
\end{column}
\begin{column}{0.5\textwidth}
\begin{adjustbox}{max totalsize={\textwidth},center}
\begin{tikzpicture}
\begin{axis}
[
title={Contour plot, view from top},
view={0}{90},
xlabel=$x$,
ylabel=$y$,
axis x line*=bottom,
axis y line*=left,
xtick align=outside,
ytick align=outside,
unit vector ratio*=1 1 1,
]
\addplot3[
contour gnuplot={number=14,}
]
{x^2};
\addplot[only marks, mark=*]
coordinates{ % plot 1 data set
(%f,%f)
};
\end{axis}
\end{tikzpicture}
\end{adjustbox}
\end{column}
\end{columns}
\end{frame}
""" %(i, i, i, i, i)--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-10-3f4f6db3ccf0> in <module> 71 72 \end{frame} ---> 73 """ %(i, i, i, i, i) ValueError: unsupported format character 'p' (0x70) at index 793
s = ""
for i in range(iterations):
s+="\\begin{frame}{Gradient Descent}\n"
s+=" \\begin{center}\n"
s+=" \includegraphics[totalheight=6cm]{gradient-descent/iteration-"+str(i+1)+".eps}\n"
s+=" \end{center}\n"
s+="\end{frame}\n\n"print (s)\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-1.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-2.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-3.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-4.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-5.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-6.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-7.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-8.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-9.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-10.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-11.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-12.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-13.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-14.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-15.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-16.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-17.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-18.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-19.eps}
\end{center}
\end{frame}
\begin{frame}{Gradient Descent}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/iteration-20.eps}
\end{center}
\end{frame}
8.2*4.133.62def func(x):
return np.sin(x) + np.sin(x/2) + np.sin(x/3)fig, ax = plt.subplots()
x = np.linspace(-10,10,100)
x = x[x<=0]
y = func(x)
latexify()
val = -7.2
plt.scatter([val],func(np.array([val])), color='k')
ax.annotate('Local minima', xy=(val, func(val)), xytext=(val, 1),
arrowprops=dict(facecolor='grey', shrink=0.0001))
plt.xticks([])
plt.yticks([])
plt.plot(x,y, color='grey')
format_axes(plt.gca())
plt.xlabel("x")
plt.ylabel("y=f(x)")
plt.savefig("../gradient-descent/local-minima.eps", format='eps',transparent=True, bbox_inches="tight")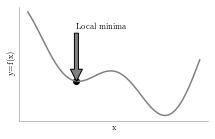
import sys
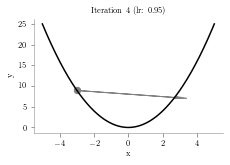
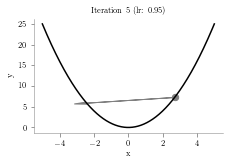
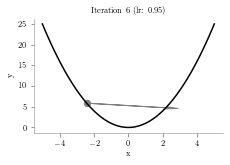
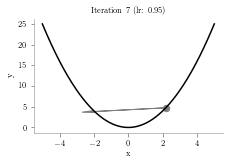
sys.path.append("../")from latexify import format_axes, latexifyx = np.linspace(-5,5,1000)
y = x**2
p = 4.1
alpha = 0.95
iterations = 10
latexify()
# for i in range(10):
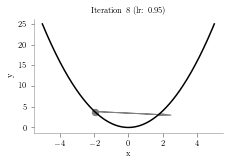
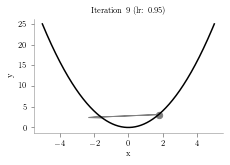
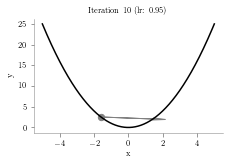
for i in range(iterations):
plt.figure()
plt.plot(x,y,'k')
prev = p
p = p - (alpha*2*p)
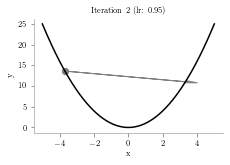
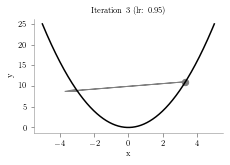
plt.arrow(prev,prev**2,p-prev,p**2-prev**2,head_width=0.5, color='grey')
plt.scatter([prev],[prev**2],s=40, color='grey')
plt.xlabel("x")
plt.ylabel("y")
plt.title("Iteration "+str(i+1)+" (lr: "+str(alpha)+")")
format_axes(plt.gca())
plt.savefig("../gradient-descent/overshooting-"+str(i+1)+".eps", format='eps',transparent=True, bbox_inches="tight")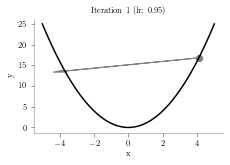
s = ""
for i in range(iterations):
s+="\\begin{frame}{Overshooting}\n"
s+=" \\begin{center}\n"
s+=" \includegraphics[totalheight=6cm]{gradient-descent/overshooting-"+str(i+1)+".eps}\n"
s+=" \end{center}\n"
s+="\end{frame}\n\n"print (s)\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-1.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-2.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-3.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-4.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-5.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-6.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-7.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-8.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-9.eps}
\end{center}
\end{frame}
\begin{frame}{Overshooting}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/overshooting-10.eps}
\end{center}
\end{frame}
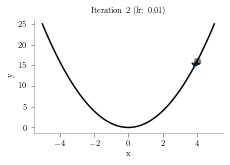
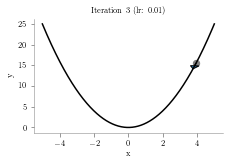
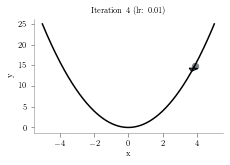
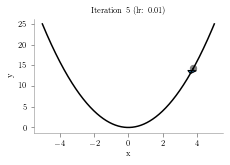
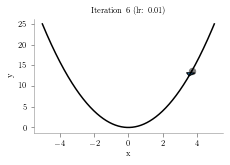
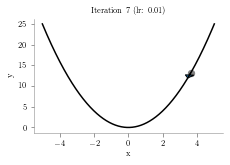
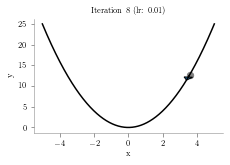
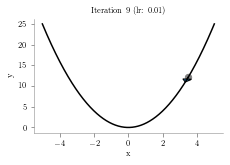
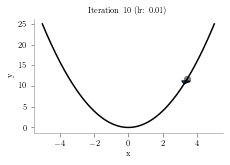
x = np.linspace(-5,5,1000)
y = x**2
p = 4.1
alpha = .01
iterations = 10
latexify()
# for i in range(10):
for i in range(iterations):
plt.figure()
plt.plot(x,y,'k')
prev = p
p = p - (alpha*2*p)
plt.arrow(prev,prev**2,p-prev,p**2-prev**2,head_width=0.5)
plt.scatter([prev],[prev**2],s=40, color='grey')
plt.xlabel("x")
plt.ylabel("y")
plt.title("Iteration "+str(i+1)+" (lr: "+str(alpha)+")")
format_axes(plt.gca())
plt.savefig("../gradient-descent/undershooting-"+str(i+1)+".eps", format='eps',transparent=True, bbox_inches="tight")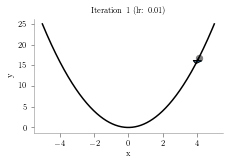
s = ""
for i in range(iterations):
s+="\\begin{frame}{Slow Convergence}\n"
s+=" \\begin{center}\n"
s+=" \includegraphics[totalheight=6cm]{gradient-descent/undershooting-"+str(i+1)+".eps}\n"
s+=" \end{center}\n"
s+="\end{frame}\n\n"print (s)\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-1.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-2.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-3.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-4.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-5.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-6.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-7.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-8.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-9.eps}
\end{center}
\end{frame}
\begin{frame}{Slow Convergence}
\begin{center}
\includegraphics[totalheight=6cm]{gradient-descent/undershooting-10.eps}
\end{center}
\end{frame}
x = np.linspace(-5,5,1000)
y = x**2
p = 4.1
alpha = .01
iterations = 10
latexify()
# for i in range(10):
for i in range(iterations):
plt.figure()
plt.plot(x,y,'k')
prev = p
p = p - (alpha*2*p)
plt.arrow(prev,prev**2,p-prev,p**2-prev**2,head_width=0.5)
plt.scatter([prev],[prev**2],s=40, color='grey')
plt.xlabel("x")
plt.ylabel("y")
plt.title("Iteration "+str(i+1)+" (lr: "+str(alpha)+")")
format_axes(plt.gca())
plt.savefig("../gradient-descent/undershooting-"+str(i+1)+".eps", format='eps',transparent=True, bbox_inches="tight")x = np.linspace(1,10,100)
y = 1/x
plt.plot(y,label="GD")
noise = np.random.random((len(x)))
noise[0] = 0
noise[1] = 0
noise[2] = 0
plt.plot(y+0.2*(noise-0.5),label="SGD")
plt.legend()
plt.title("Iterations vs Cost")
plt.xlabel("Iteration")
plt.ylabel("Cost")
plt.savefig("gd-sgd.eps", format='eps',transparent=True)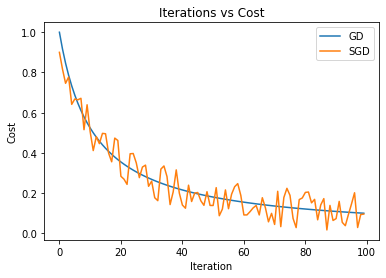
val = 4.1
alpha = 0.05
for i in range(10):
val = val - alpha * 2* val
print (val)3.6899999999999995
3.3209999999999997
2.9888999999999997
2.6900099999999996
2.4210089999999997
2.1789080999999997
1.9610172899999996
1.7649155609999996
1.5884240048999996
1.4295816044099996