SVM implementation using CVXOpt

SVM using CVXOpt

Author

Nipun Batra

Published

April 12, 2024

This post is pretty much borrowed with slight modifications from this excellent blog post from Matthieu Blondel

General QP problem

A general QP problem can be formulated as follows:

\[ \begin{align*} \text{minimize} \quad & \frac{1}{2} x^T P x + q^T x \\ \text{subject to} \quad & G x \leq h \\ & A x = b \end{align*} \]

Solving in Dual

In dual in hard margin SVM, the dual problem is formulated as follows:

\[ \begin{align*} \text{maximize} \quad & \sum_{i=1}^{m} \alpha_i - \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_i \alpha_j y^{(i)} y^{(j)} (x^{(i)})^T x^{(j)} \\ \text{subject to} \quad & \alpha_i \geq 0 \quad \text{for} \quad i = 1, 2, \ldots, m \\ & \sum_{i=1}^{m} \alpha_i y^{(i)} = 0 \end{align*} \]

Or, we can write it in the following form (minimization problem): \[ \begin{align*} \text{minimize} \quad & \frac{1}{2} \alpha^T Q \alpha + e^T \alpha \\ \text{subject to} \quad & y^T \alpha = 0 \\ & \alpha \geq 0 \end{align*} \]

where \[ \begin{align*} Q_{ij} & = y^{(i)} y^{(j)} (x^{(i)})^T x^{(j)} \\ e_i & = -1 \end{align*} \]

we can again write it in the following form using kernel trick:

\[ Q_{ij} = y^{(i)} y^{(j)} K(x^{(i)}, x^{(j)}) \]

where \(K(x^{(i)}, x^{(j)}) = (x^{(i)})^T x^{(j)}\) is the kernel function.

Thus, we can now set \[ \begin{align*} P & = Q \\ q & = e \\ G & = -I \\ h & = 0 \\ A & = y^T \\ b & = 0 \end{align*} \]

where \(I\) is the identity matrix.

try: 
    import cvxopt
    import cvxopt.solvers

except:
    %pip install cvxopt
    import cvxopt
    import cvxopt.solvers

import numpy as np
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

def linear_kernel(x1, x2):
    return np.dot(x1, x2)

def polynomial_kernel(x, y, p=3):
    return (1 + np.dot(x, y)) ** p

def gaussian_kernel(x, y, sigma=5.0):
    return np.exp(-np.linalg.norm(x-y)**2 / (2 * (sigma ** 2)))

X, y = make_blobs(n_samples=40, centers=2, n_features=2, random_state=42)

y[y == 0] = -1.0
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)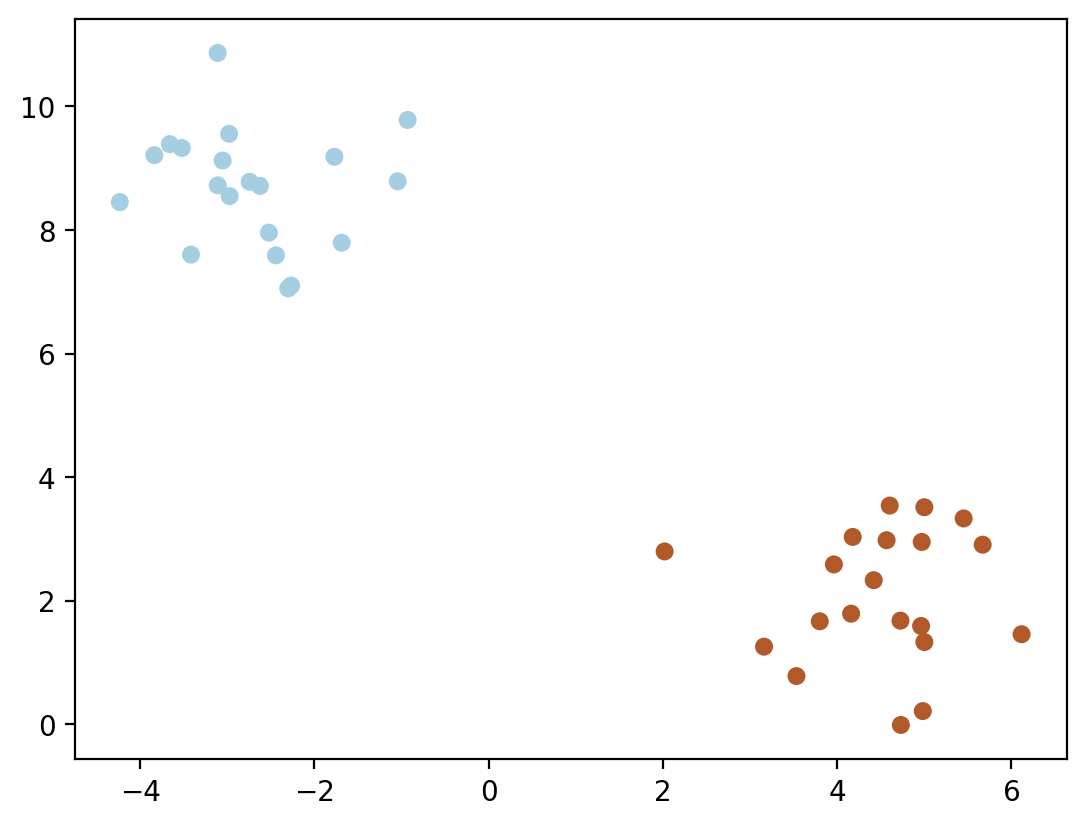

n_samples, n_features = X.shape
kernel = linear_kernel

# Gram matrix
K = np.zeros((n_samples, n_samples))
for i in range(n_samples):
    for j in range(n_samples):
        K[i,j] = kernel(X[i], X[j])

# QP problem formulation
P = cvxopt.matrix(np.outer(y, y) * K)
q = cvxopt.matrix(-np.ones(n_samples))
A = cvxopt.matrix(y, (1, n_samples), 'd')
b = cvxopt.matrix(0.0)
G = cvxopt.matrix(-np.eye(n_samples))
h = cvxopt.matrix(np.zeros(n_samples))

dictionary = {"P": P, "q": q, "A": A, "b": b, "G": G, "h": h}
for key, val in dictionary.items():
    print(key, val.size)

P (40, 40)
q (40, 1)
A (1, 40)
b (1, 1)
G (40, 40)
h (40, 1)

solution = cvxopt.solvers.qp(P, q, G, h, A, b)

     pcost       dcost       gap    pres   dres
 0: -1.4386e+00 -2.2358e+00  8e+01  8e+00  2e+00
 1: -5.3423e-01 -2.0710e-01  6e+00  7e-01  1e-01
 2:  3.5560e-03 -1.3362e-01  1e-01  4e-16  6e-15
 3: -3.7579e-02 -5.5490e-02  2e-02  4e-17  7e-16
 4: -5.0978e-02 -5.6104e-02  5e-03  9e-19  6e-16
 5: -5.4114e-02 -5.4359e-02  2e-04  1e-17  6e-16
 6: -5.4321e-02 -5.4336e-02  1e-05  7e-18  8e-16
 7: -5.4333e-02 -5.4333e-02  1e-07  1e-17  7e-16
 8: -5.4333e-02 -5.4333e-02  1e-09  2e-17  6e-16
Optimal solution found.

alphas_sol = np.array(solution['x']).flatten()
alphas_sol

array([4.81116795e-11, 5.57561687e-11, 4.14022254e-11, 5.64570278e-11,
       3.19971594e-11, 1.13766765e-09, 1.10946709e-10, 5.43328120e-02,
       9.43563733e-11, 3.59644883e-11, 2.72365634e-11, 1.78702226e-08,
       7.91651647e-11, 4.45973348e-11, 6.48044988e-11, 3.09926966e-11,
       3.26557350e-11, 4.12118866e-11, 2.53367783e-10, 4.55829611e-11,
       4.43685787e-11, 6.12190291e-11, 5.72210101e-11, 3.48077854e-11,
       2.70414582e-11, 3.72073366e-11, 4.52326326e-11, 6.21623048e-11,
       3.61239404e-11, 3.61946755e-11, 2.70499880e-11, 6.76419169e-11,
       3.77922165e-11, 9.70279801e-11, 4.63391531e-11, 6.74255180e-11,
       3.77950852e-11, 5.47202347e-11, 5.02000180e-11, 5.43328313e-02])

alphas_sol[alphas_sol > 1e-5]

array([0.05433281, 0.05433283])

# Support vectors have non zero lagrange multipliers
sv = alphas_sol > 1e-5
ind = np.arange(len(alphas_sol))[sv]
a = alphas_sol[sv]
sv_x = X[sv]
sv_y = y[sv]

# Plot the support vectors
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)

# Mark the support vectors with thick black circles
plt.scatter(sv_x[:, 0], sv_x[:, 1], c=sv_y, s=100, cmap=plt.cm.Paired, marker='o', edgecolors='k')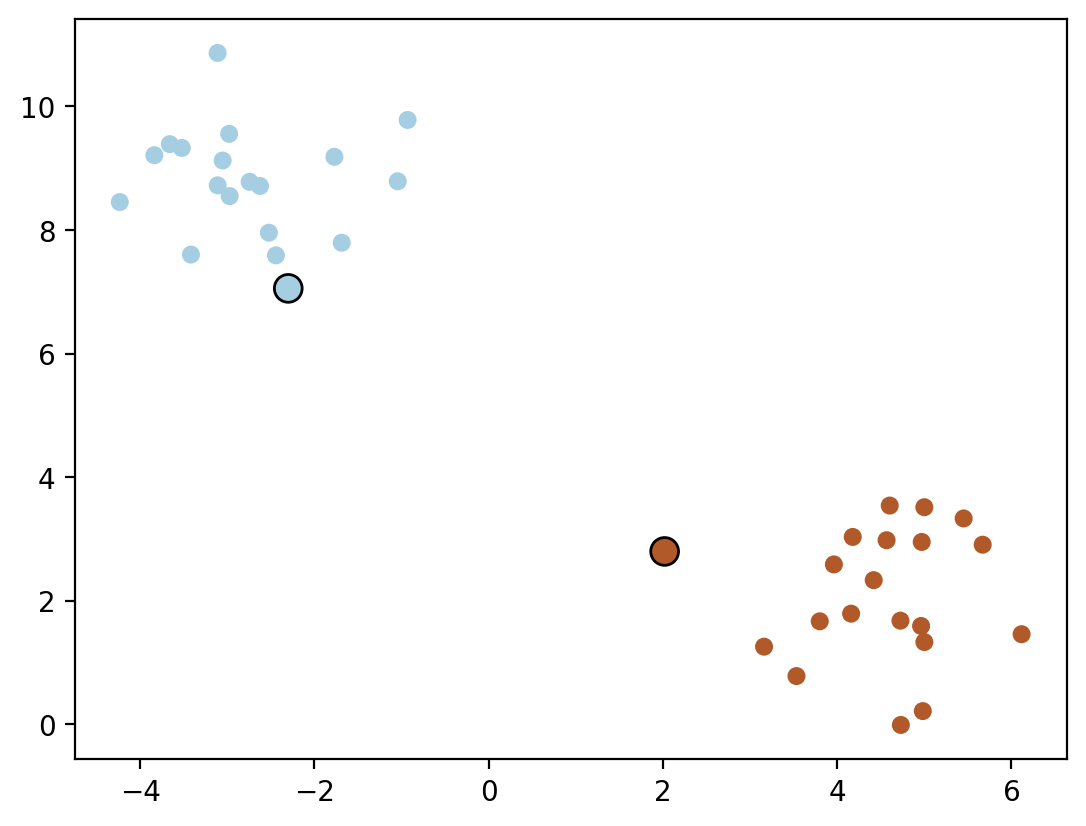

w = np.sum(a * sv_y[:, None] * sv_x, axis=0)
w

array([ 0.23474316, -0.23143308])

b = np.sum(sv_y - np.dot(sv_x, w)) / len(sv_y)
b

1.1726593683601716

# Plot the decision boundary and margins
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.Paired)
plt.scatter(sv_x[:, 0], sv_x[:, 1], c=sv_y, s=100, cmap=plt.cm.Paired, marker='o', edgecolors='k')

x_min = np.min(X[:, 0])
x_max = np.max(X[:, 0])

y_min = (-w[0] * x_min - b) / w[1]
y_max = (-w[0] * x_max - b) / w[1]

plt.plot([x_min, x_max], [y_min, y_max], 'k-')

# Margin 1
y_min = (-w[0] * x_min - b + 1) / w[1]
y_max = (-w[0] * x_max - b + 1) / w[1]

plt.plot([x_min, x_max], [y_min, y_max], 'k--')

# Margin 2
y_min = (-w[0] * x_min - b - 1) / w[1]
y_max = (-w[0] * x_max - b - 1) / w[1]

plt.plot([x_min, x_max], [y_min, y_max], 'k--')

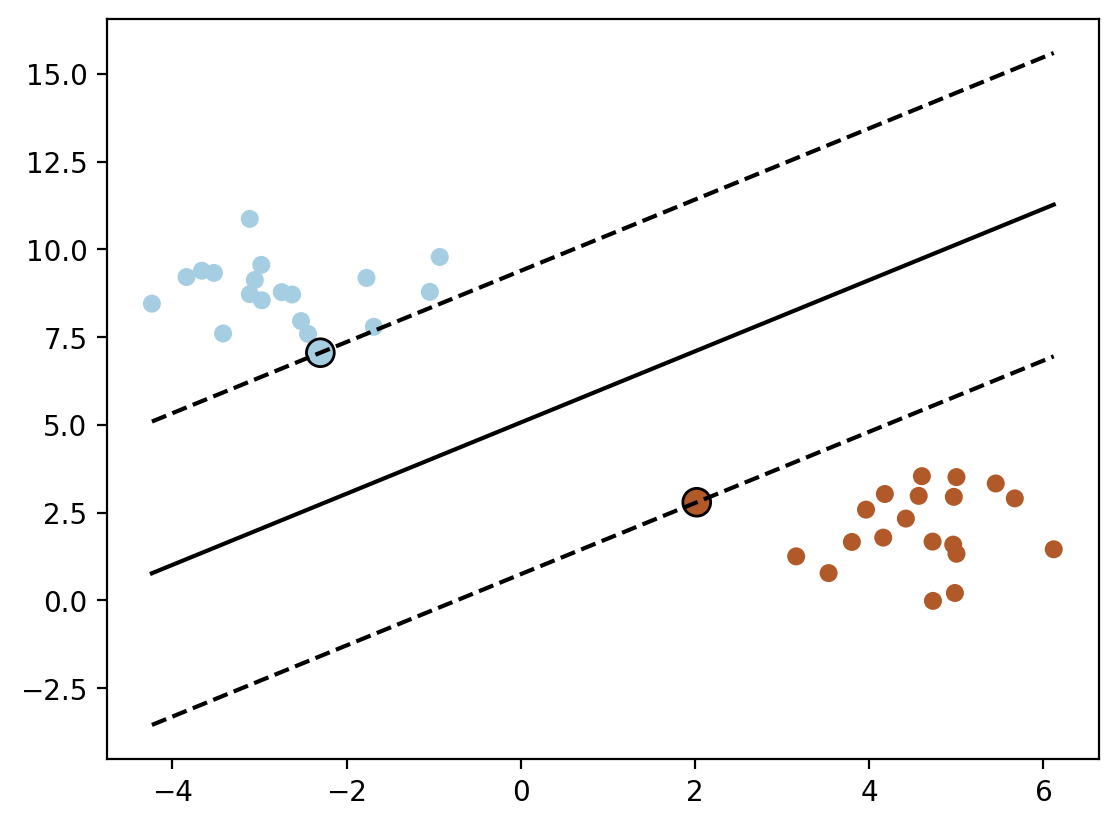
Using cvxpy

import cvxpy as cp

alpha = cp.Variable(n_samples)

inequality_constraints = [alpha >= 0]
equality_constraints = [cp.multiply(alpha, y) == 0]

overall_constraints = inequality_constraints + equality_constraints
P_numpy = np.outer(y, y)* K   + 3e-8 * np.eye(n_samples)
objective = cp.Maximize(cp.sum(alpha) - 0.5 * cp.quad_form(alpha, P_numpy))

prob = cp.Problem(objective, overall_constraints)
result = prob.solve()

prob.status
alpha.value.sort()
alpha.value

array([-1.49664286e-08, -7.86036073e-09, -7.48959975e-09, -4.95631234e-09,
       -4.80337014e-09, -4.21382858e-09, -4.17627547e-09, -3.60319297e-09,
       -2.54786233e-09, -1.86476801e-09, -1.28264318e-09, -6.50572915e-10,
       -3.44845584e-10, -4.45332158e-11,  2.50213529e-10,  2.67913419e-10,
        8.79522453e-10,  8.82710270e-10,  9.50098303e-10,  1.82268844e-09,
        2.74355414e-09,  3.45032195e-09,  4.95527787e-09,  5.02308218e-09,
        5.34165002e-09,  6.71939414e-09,  6.94177696e-09,  7.06890144e-09,
        9.38395895e-09,  9.49925189e-09,  9.72666606e-09,  1.15208492e-08,
        1.18351650e-08,  1.20920336e-08,  1.22215620e-08,  1.69516039e-08,
        2.28584041e-08,  3.45155480e-08,  5.49049991e-08,  1.01339280e-07])

Primal using cvxopt

# Number of features
n_features = X.shape[1]

# Identity matrix
P = cvxopt.matrix(np.block([[np.eye(n_features), np.zeros((n_features, 1))], [np.zeros((1, n_features + 1))]]))

# Inequality constraints matrix
G = cvxopt.matrix(-np.block([np.diag(y) @ X, y.reshape(-1, 1)]))

# Inequality constraints bounds
h = cvxopt.matrix(-np.ones(X.shape[0]))

# Solve the QP problem
solution = cvxopt.solvers.qp(P, cvxopt.matrix(np.zeros(n_features + 1)), G, h)

# Extract optimized w and b values
w_opt = np.array(solution['x'][:-1])
b_opt = np.array(solution['x'][-1])

     pcost       dcost       gap    pres   dres
 0:  1.9726e-02  3.3304e+00  8e+01  2e+00  3e+02
 1:  1.2482e-01 -5.6113e+00  6e+00  1e-01  2e+01
 2:  1.3362e-01 -3.5560e-03  1e-01  4e-16  5e-15
 3:  5.5490e-02  3.7579e-02  2e-02  3e-16  3e-16
 4:  5.6104e-02  5.0978e-02  5e-03  2e-16  1e-16
 5:  5.4359e-02  5.4114e-02  2e-04  2e-16  1e-16
 6:  5.4336e-02  5.4321e-02  1e-05  2e-16  2e-15
 7:  5.4333e-02  5.4333e-02  1e-07  3e-16  2e-16
 8:  5.4333e-02  5.4333e-02  1e-09  2e-16  3e-16
Optimal solution found.

w_opt, w

(array([[ 0.23474325],
        [-0.23143308]]),
 array([ 0.23474316, -0.23143308]))

b_opt, b

(array(1.17265942), 1.1726593683601716)