SVM Kernel

Author

Nipun Batra

Published

April 20, 2023

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import cm
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

X = np.array([-2, -1, 0, 1, 2, 3, 4]).reshape(-1, 1)
y = np.array([-1, -1, 1, 1, 1, -1, -1])

plt.scatter(X.flatten(), np.zeros_like(X), c=y, cmap=cm.Paired)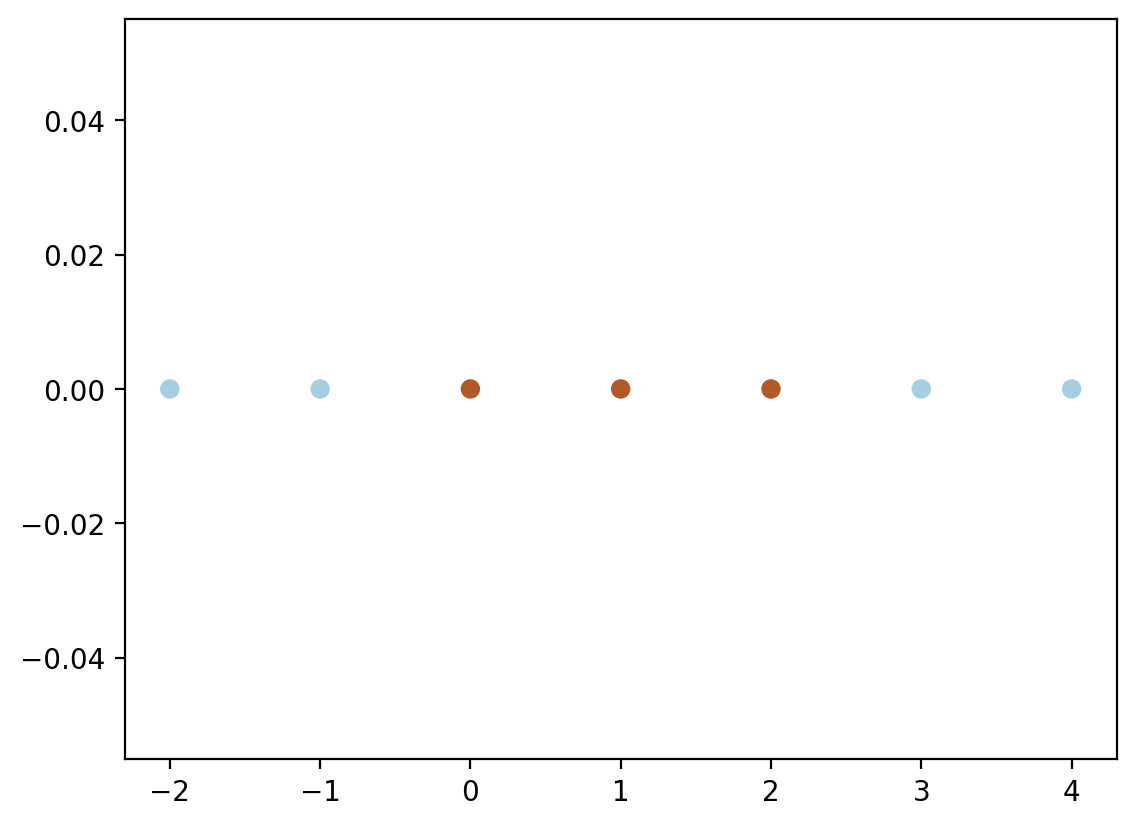

def phi(x):
    return np.hstack([x, x**2])

phi(X)

array([[-2,  4],
       [-1,  1],
       [ 0,  0],
       [ 1,  1],
       [ 2,  4],
       [ 3,  9],
       [ 4, 16]])

plt.scatter(phi(X)[:, 0], phi(X)[:, 1], c = y,cmap = cm.Paired)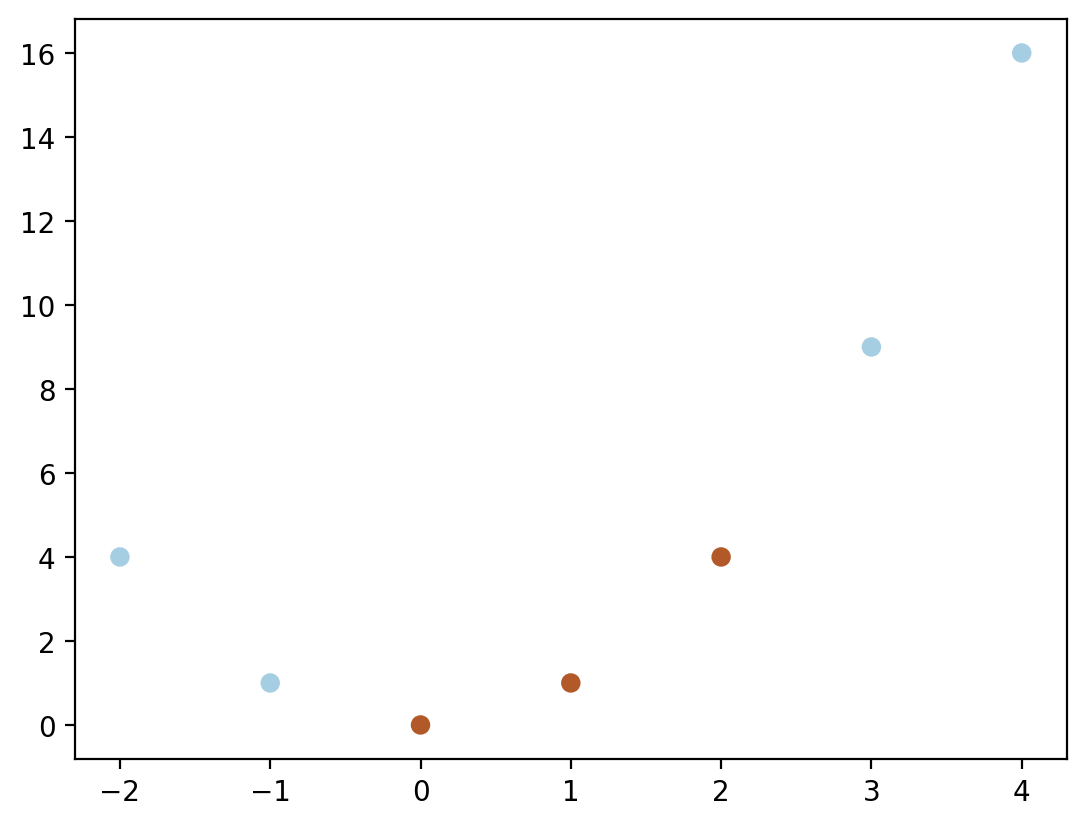

from sklearn.svm import SVC

c = SVC(kernel='linear', C = 1e6)

c.fit(phi(X), y)

SVC(C=1000000.0, kernel='linear')

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

plt.scatter(phi(X)[:, 0], phi(X)[:, 1], c = y, zorder=10, cmap =cm.Paired, edgecolors='k', alpha=1, s=200)
x_min = phi(X)[:, 0].min()-1
x_max = phi(X)[:, 0].max()+1
y_min = phi(X)[:, 1].min()-1
y_max = phi(X)[:, 1].max()+1

XX, YY = np.mgrid[x_min:x_max:200j, y_min:y_max:200j]
Z = c.decision_function(np.c_[XX.ravel(), YY.ravel()])

# Put the result into a color plot
Z = Z.reshape(XX.shape)
plt.pcolormesh(XX, YY, Z > 0, cmap=plt.cm.Paired, alpha=0.6)
plt.contour(XX, YY, Z, colors=['k', 'k', 'k'],
            linestyles=['--', '-', '--'], levels=[-1, 0, 1])
plt.xlabel(r"$x_1 = X$")
plt.ylabel(r"$x_2 = X^2$")
plt.title(r"Decision surface: {:0.1f}*x_1 + {:0.1f}*x_2 + {:0.1f} = 0".format(c.coef_[0, 0], c.coef_[0, 1], c.intercept_[0]))

Text(0.5, 1.0, 'Decision surface: 1.3*x_1 + -0.7*x_2 + 1.0 = 0')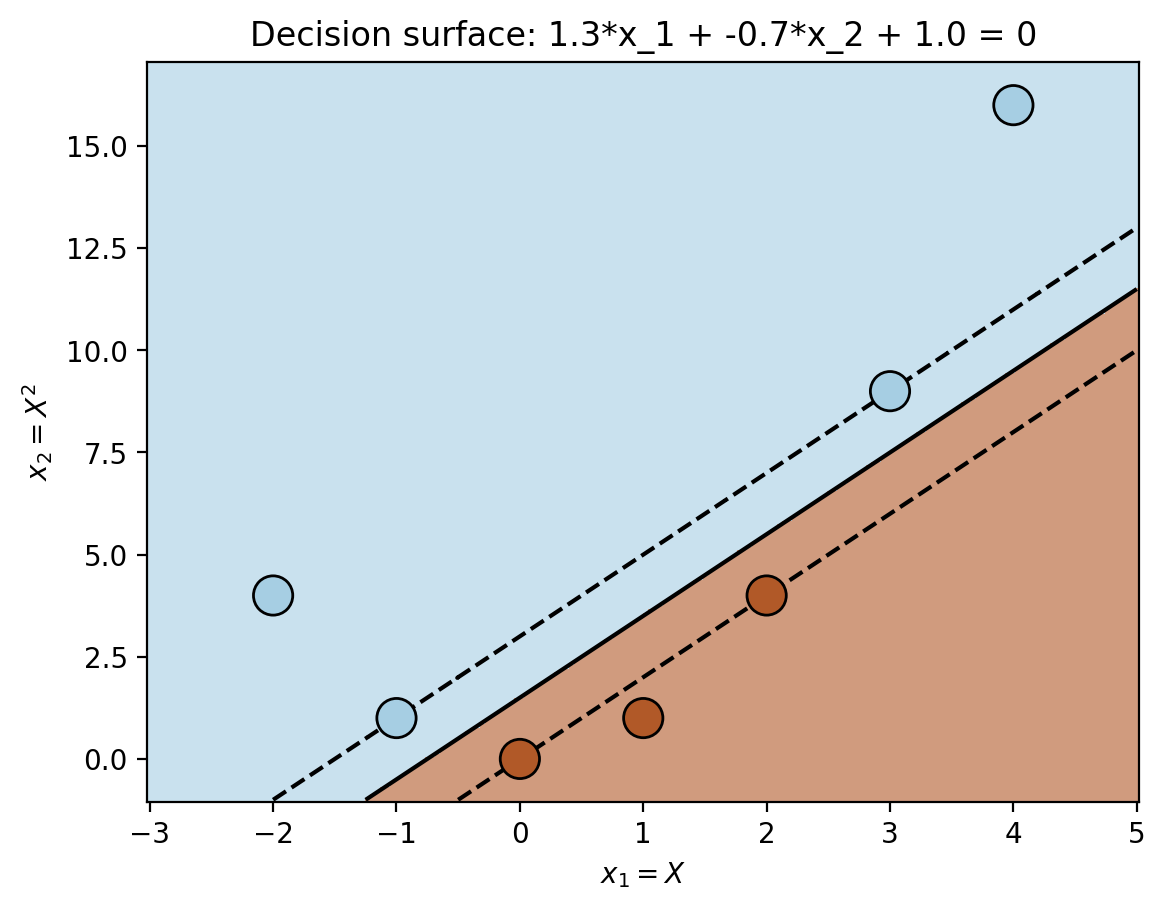

# Now using non-linearly separable data in 2D

from sklearn.datasets import make_blobs, make_circles

X, y = make_circles(n_samples=100, factor=0.5, noise=0.4)

plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cm.Paired)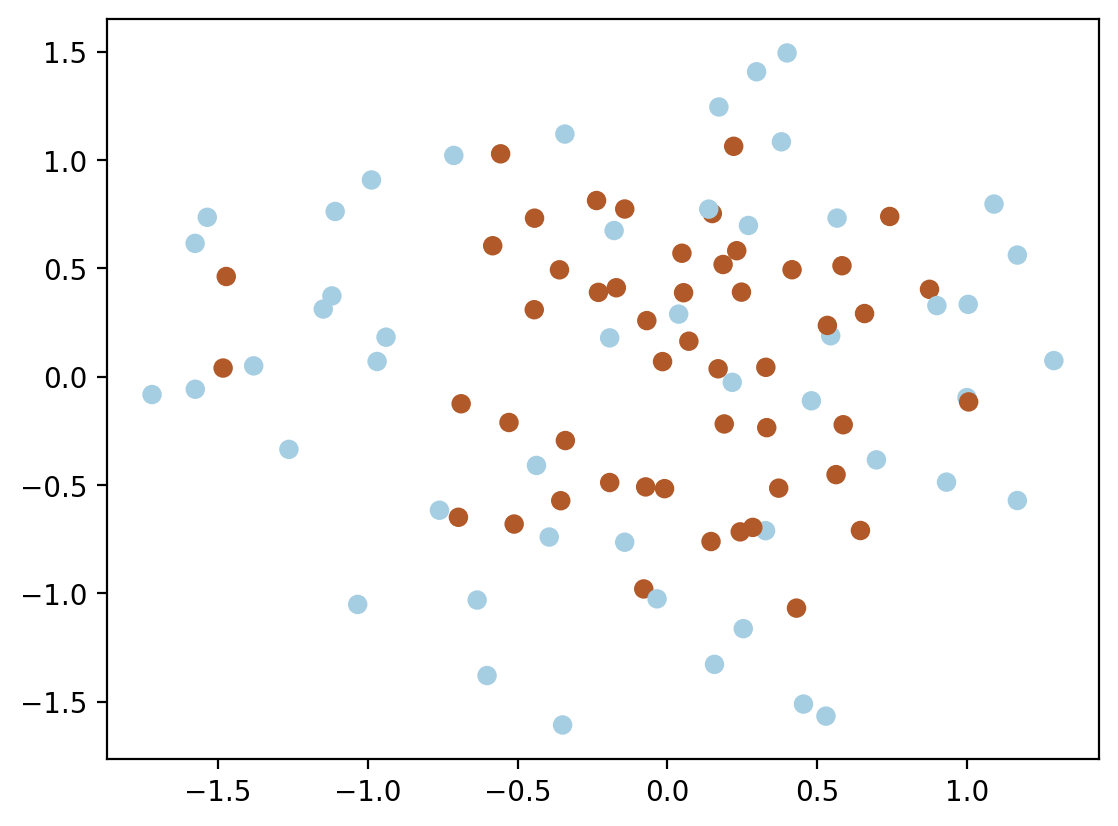

def plot_contour(X, y, clf):
    xx, yy = np.meshgrid(np.linspace(X[:, 0].min(), X[:, 0].max(), 40), np.linspace(X[:, 1].min(), X[:, 1].max(), 40))
    Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.9,
            linestyles=['--', '-', '--'])

    plt.scatter(c.support_vectors_[:, 0], c.support_vectors_[:, 1], s=100,
            linewidth=1, facecolors='none', edgecolors='k')
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cm.Paired)
    
    plt.pcolormesh(xx, yy, Z > 0, cmap=plt.cm.Paired, alpha=0.2)

    
    
    # Train accuracy
    y_pred = clf.predict(X)
    plt.title("Train accuracy: {:0.2f}\n Number of support vectors: {}".format((y_pred == y).mean(), len(clf.support_vectors_)))

# First linear SVM

c = SVC(kernel='linear', C=10)
c.fit(X, y)

plot_contour(X, y, c)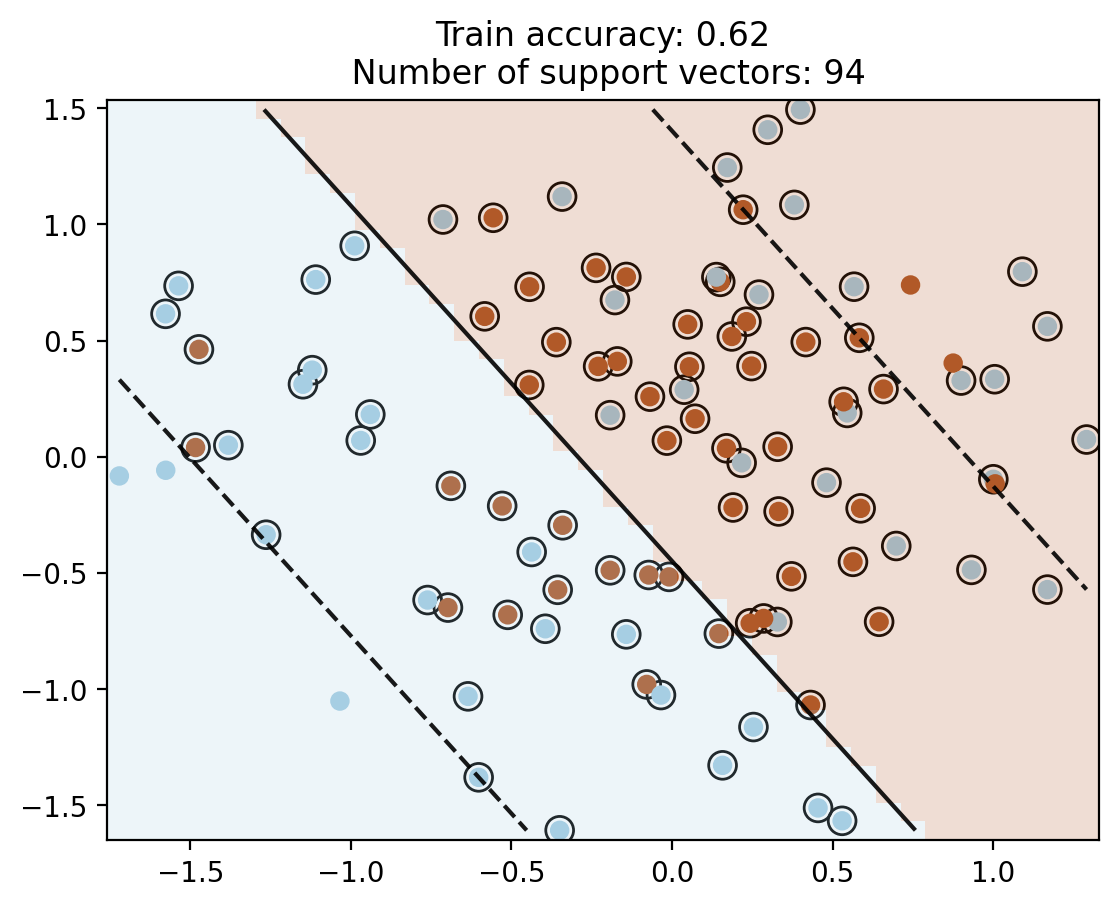

c_poly2 = SVC(kernel='poly', degree=2, C=10)

c_poly2.fit(X, y)

plot_contour(X, y, c_poly2)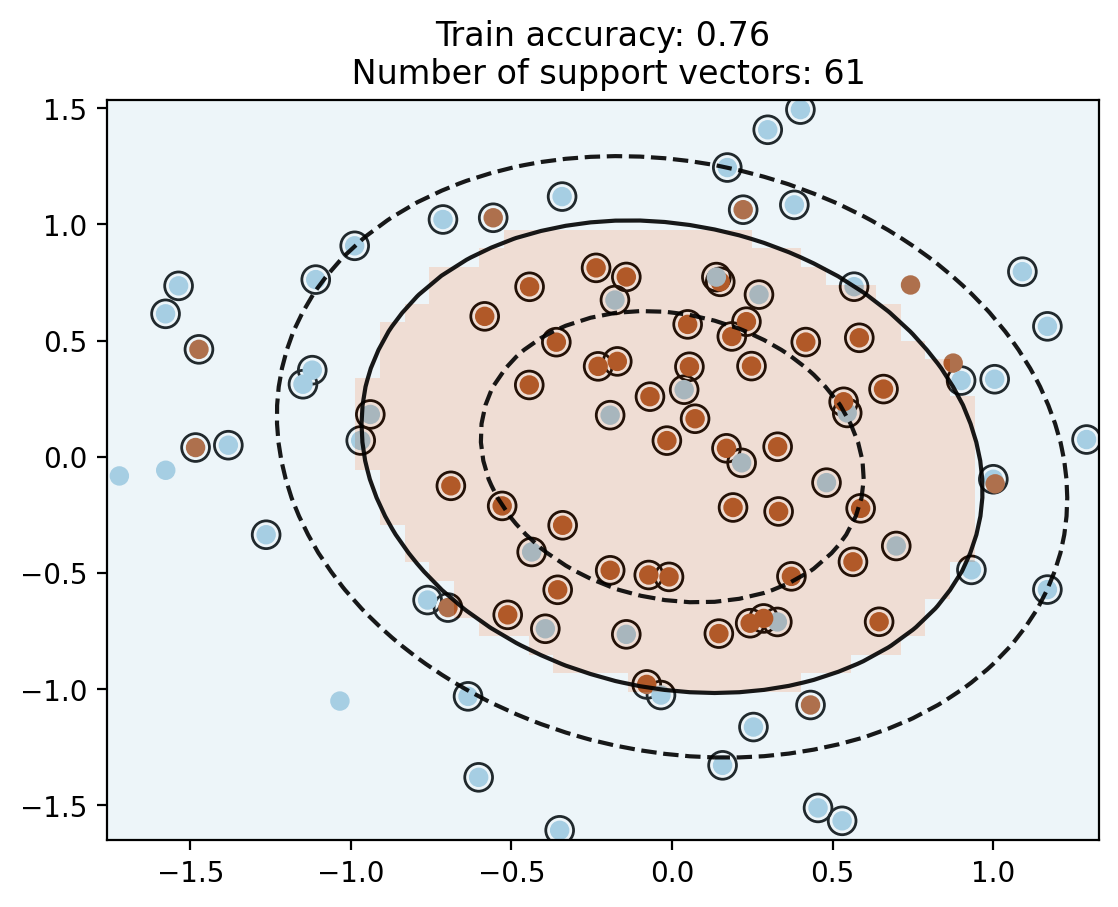

# RBF kernel

c_rbf = SVC(kernel='rbf', C=10, gamma=1e-1)
c_rbf.fit(X, y)

plot_contour(X, y, c_rbf)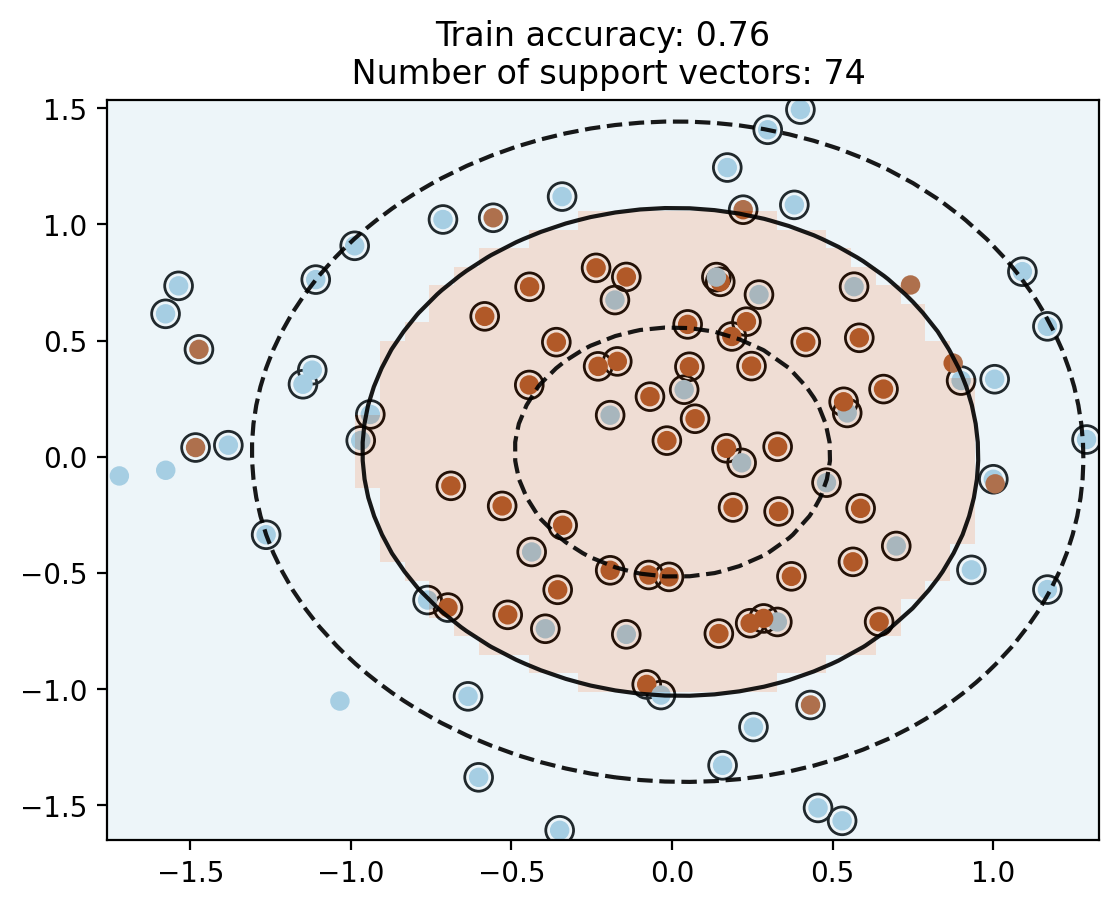

# interactive widget to show the effect of gamma

from ipywidgets import interact

def plot_svm(gamma=0.05):
    c = SVC(kernel='rbf', C=10, gamma=gamma)
    c.fit(X, y)
    plot_contour(X, y, c)

interact(plot_svm, gamma=(0.01, 60, 0.05))

<function __main__.plot_svm(gamma=0.05)>