Probabilistic Machine Learning – mcmc-hamiltorch

import os
os.environ["CUDA_VISIBLE_DEVICES"] = "3"

import torch
import torch.autograd.functional as F
import torch.distributions as dist

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

import pandas as pd
%matplotlib inline

# Retina display
%config InlineBackend.figure_format = 'retina'

from tueplots import bundles

plt.rcParams.update(bundles.beamer_moml())
# plt.rcParams.update(bundles.icml2022())


# Also add despine to the bundle using rcParams
plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False

# Increase font size to match Beamer template
plt.rcParams["font.size"] = 16
# Make background transparent
plt.rcParams["figure.facecolor"] = "none"

import hamiltorch

hamiltorch.set_random_seed(123)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

device

device(type='cuda')

gt_distribution = torch.distributions.Normal(0, 1)


# Samples from the ground truth distribution
def sample_gt(n):
    return gt_distribution.sample((n,))


samples = sample_gt(1000)

x_lin = torch.linspace(-3, 3, 1000)
y_lin = torch.exp(gt_distribution.log_prob(x_lin))

plt.plot(x_lin, y_lin, label="Ground truth")
plt.legend()

<matplotlib.legend.Legend at 0x7fb356939c40>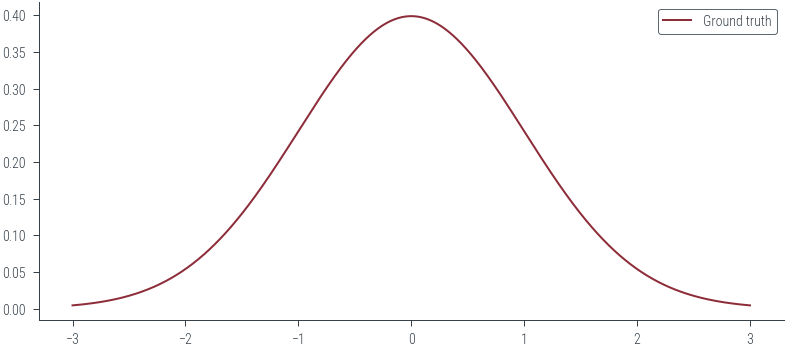

# Logprob function to be passed to Hamiltorch sampler
def logprob(x):
    return gt_distribution.log_prob(x)

logprob(torch.tensor([0.0]))

tensor([-0.9189])

# Initial state
x0 = torch.tensor([0.0])
num_samples = 5000
step_size = 0.3
num_steps_per_sample = 5
hamiltorch.set_random_seed(123)

params_hmc = hamiltorch.sample(
    log_prob_func=logprob,
    params_init=x0,
    num_samples=num_samples,
    step_size=step_size,
    num_steps_per_sample=num_steps_per_sample,
)

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:07 | 0d:00:00:00 | #################### | 5000/5000 | 698.22       
Acceptance Rate 0.99

params_hmc = torch.tensor(params_hmc)

# Trace plot
plt.plot(params_hmc, label="Trace")
plt.xlabel("Iteration")
plt.ylabel("Parameter value")

Text(0, 0.5, 'Parameter value')

# view first 500 samples
plt.plot(params_hmc[:500], label="Trace")
plt.xlabel("Iteration")
plt.ylabel("Parameter value")

Text(0, 0.5, 'Parameter value')

# KDE plot
import seaborn as sns

plt.figure()
sns.kdeplot(params_hmc.detach().numpy(), label="Samples", shade=True, color="C1")
plt.plot(x_lin, y_lin, label="Ground truth")
plt.xlabel("Parameter value")
plt.ylabel("Density")
plt.legend()

<matplotlib.legend.Legend at 0x7fb353810dc0>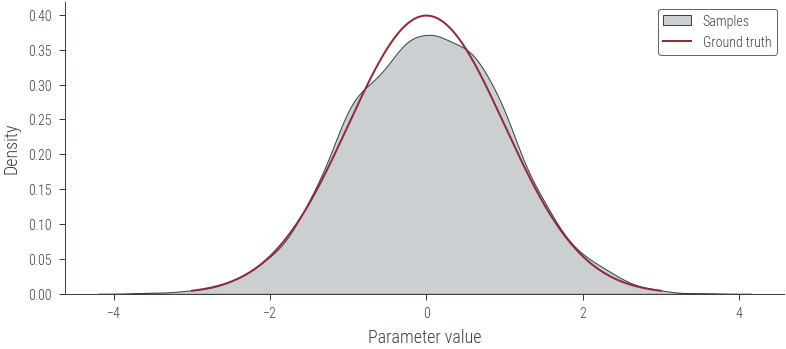

def plot_samples_gif(x_lin, y_lin, params_hmc, filename, frames=50):
    fig, ax = plt.subplots()
    plt.plot(x_lin, y_lin, label="Ground truth")
    scatter = ax.scatter([], [], color="C1", marker="x", s=100)

    # Function to update the animation
    def update(frame):
        scatter.set_offsets(np.array([[params_hmc[frame], 0]]))
        return (scatter,)

    # Create the animation
    anim = FuncAnimation(fig, update, frames=frames, blit=True)

    # Save the animation as a GIF or video file (you can change the filename and format)
    anim.save(filename, dpi=200)

plot_samples_gif(
    x_lin, y_lin, params_hmc, "../figures/sampling/mcmc/hamiltorch-samples-normal.gif"
)

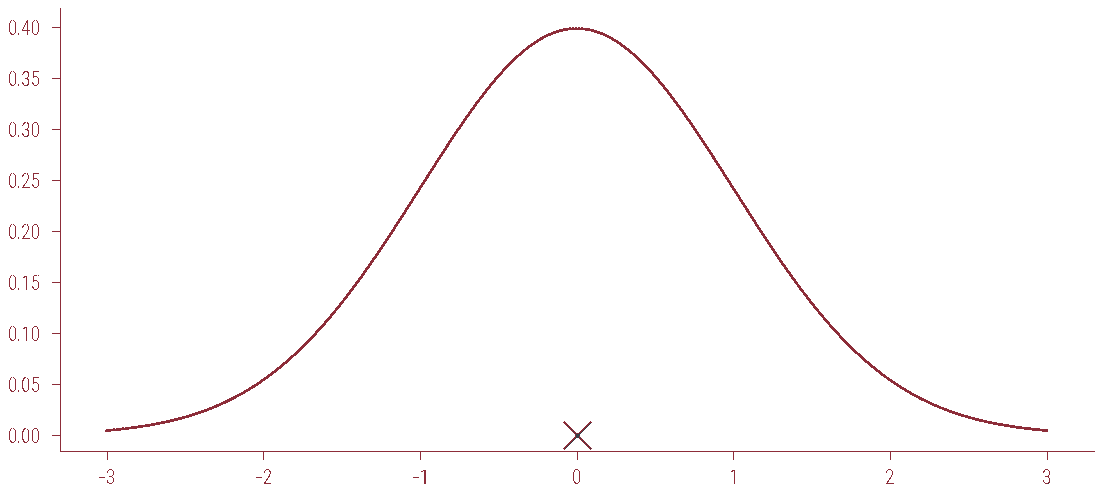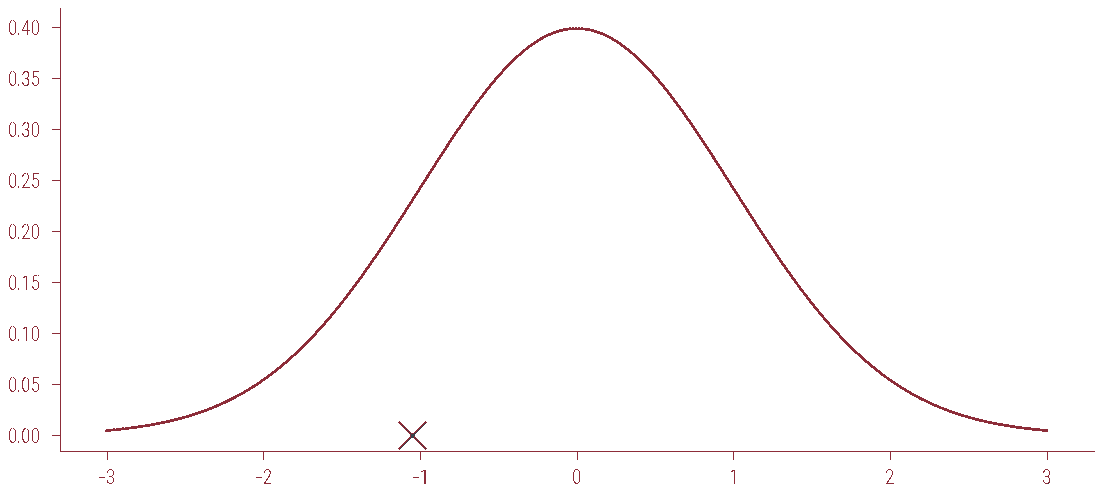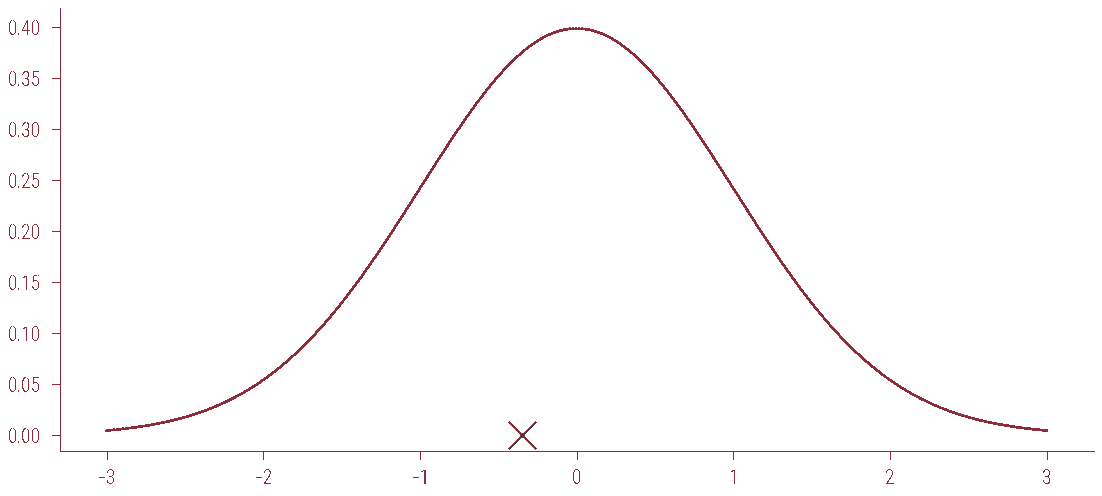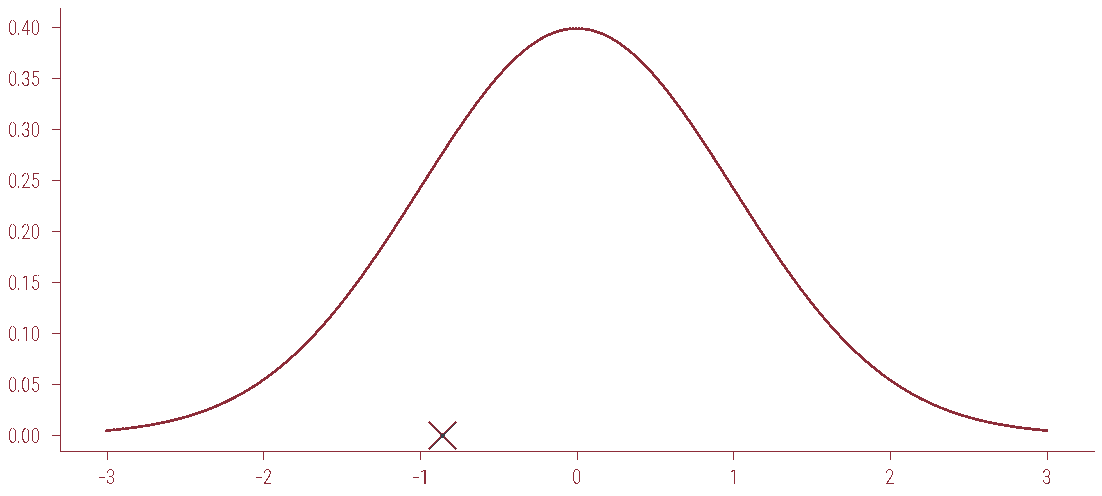
# sample from Mixture of Gaussians

mog = dist.MixtureSameFamily(
    mixture_distribution=dist.Categorical(torch.tensor([0.3, 0.7])),
    component_distribution=dist.Normal(
        torch.tensor([-2.0, 2.0]), torch.tensor([1.0, 0.5])
    ),
)

samples = mog.sample((1000,))
sns.kdeplot(samples.numpy(), label="Samples", shade=True, color="C1")

<AxesSubplot:ylabel='Density'>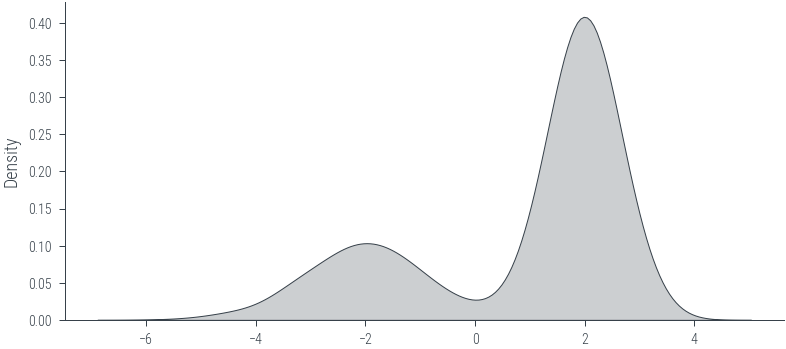

# Logprob function to be passed to Hamiltorch sampler
def logprob(x):
    return mog.log_prob(x)


logprob(torch.tensor([0.0]))

tensor([-4.1114])

# Initial state
x0 = torch.tensor([0.0])
num_samples = 5000
step_size = 0.3
num_steps_per_sample = 5
hamiltorch.set_random_seed(123)

params_hmc = hamiltorch.sample(
    log_prob_func=logprob,
    params_init=x0,
    num_samples=num_samples,
    step_size=step_size,
    num_steps_per_sample=num_steps_per_sample,
)

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:10 | 0d:00:00:00 | #################### | 5000/5000 | 462.18       
Acceptance Rate 0.99

params_hmc = torch.tensor(params_hmc)

# Trace plot
plt.plot(params_hmc[:500], label="Trace")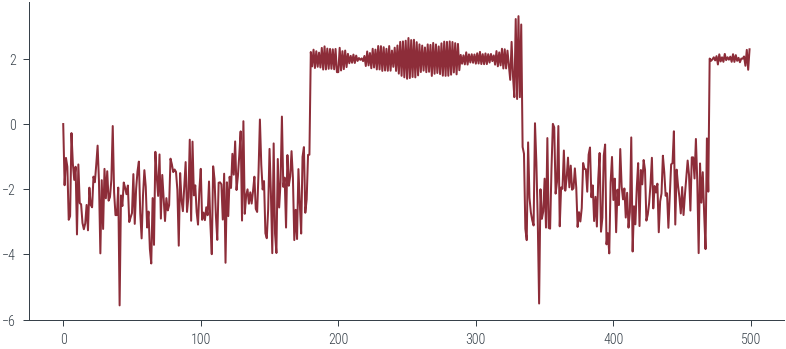

y_lin = torch.exp(mog.log_prob(x_lin))
plot_samples_gif(
    x_lin,
    y_lin,
    params_hmc,
    "../figures/sampling/mcmc/hamiltorch-samples-mog.gif",
    frames=300,
)

def p_tilde(x):
    # normalising constant for standard normal distribution
    Z = torch.sqrt(torch.tensor(2 * np.pi))
    return dist.Normal(0, 1).log_prob(x).exp() * Z


def p_tilde_log_prob(x):
    # normalising constant for standard normal distribution
    Z = torch.sqrt(torch.tensor(2 * np.pi))
    return dist.Normal(0, 1).log_prob(x) + torch.log(Z)

# Plot unnormalized distribution
x_lin = torch.linspace(-3, 3, 1000)
y_lin = p_tilde(x_lin)
plt.plot(x_lin, y_lin, label="Unnormalized distribution")
# Plot normalized distribution
plt.plot(
    x_lin, dist.Normal(0, 1).log_prob(x_lin).exp(), label="Normalized distribution"
)
plt.legend()

<matplotlib.legend.Legend at 0x7fb3378375e0>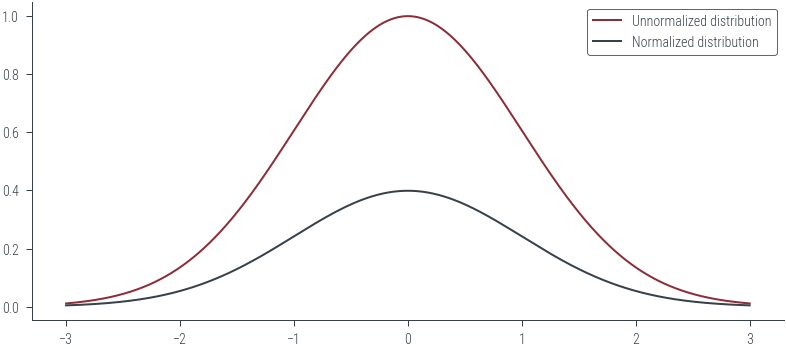

# HMC over unnormalized distribution


# Logprob function to be passed to Hamiltorch sampler
def logprob(x):
    return p_tilde_log_prob(x)

# HMC
x0 = torch.tensor([0.0])
num_samples = 5000
step_size = 0.3
num_steps_per_sample = 5
hamiltorch.set_random_seed(123)

params_hmc = hamiltorch.sample(
    log_prob_func=logprob,
    params_init=x0,
    num_samples=num_samples,
    step_size=step_size,
    num_steps_per_sample=num_steps_per_sample,
)

params_hmc = torch.tensor(params_hmc)

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:10 | 0d:00:00:00 | #################### | 5000/5000 | 488.07       
Acceptance Rate 0.99

# Trace plot
plt.plot(params_hmc[:500], label="Trace")

# KDE plot
sns.kdeplot(params_hmc.detach().numpy(), label="Samples", shade=True, color="C1")
plt.plot(x_lin, y_lin, label="Unnormalized distribution")
plt.plot(
    x_lin, dist.Normal(0, 1).log_prob(x_lin).exp(), label="Normalized distribution"
)
plt.legend()

<matplotlib.legend.Legend at 0x7fb3377450d0>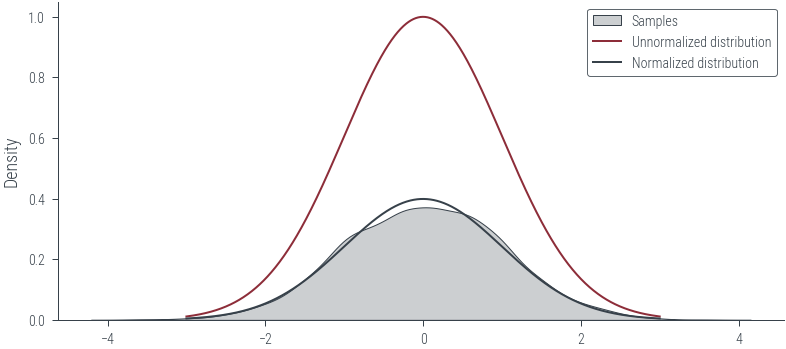

# Coin toss

prior = dist.Beta(1, 1)
data = torch.tensor([1.0, 1.0, 1.0, 0.0, 0.0])
n = len(data)


def log_prior(theta):
    return prior.log_prob(theta)


def log_likelihood(theta):
    return dist.Bernoulli(theta).log_prob(data).sum()


def negative_log_joint(theta):
    return log_prior(theta) + log_likelihood(theta)

def run_hmc(logprob, x0, num_samples, step_size, num_steps_per_sample):
    torch.manual_seed(12)
    params_hmc = hamiltorch.sample(
        log_prob_func=logprob,
        params_init=x0,
        num_samples=num_samples,
        step_size=step_size,
        num_steps_per_sample=num_steps_per_sample,
    )
    return torch.stack(params_hmc)

try:
    params_hmc_theta = run_hmc(negative_log_joint, torch.tensor([0.5]), 5000, 0.3, 5)
except Exception as e:
    print(e)

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
Expected value argument (Tensor of shape (1,)) to be within the support (Interval(lower_bound=0.0, upper_bound=1.0)) of the distribution Beta(), but found invalid values:
tensor([-0.1017], requires_grad=True)

# Let us work instead with logits
def log_prior(logits):
    return prior.log_prob(torch.sigmoid(logits)).sum()


def log_likelihood(logits):
    return dist.Bernoulli(logits=logits).log_prob(data).sum()


def log_joint(logits):
    return log_prior(logits) + log_likelihood(logits)

params_hmc_logits = run_hmc(log_joint, torch.tensor([0.0]), 1000, 0.3, 5)

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:03 | 0d:00:00:00 | #################### | 1000/1000 | 278.54       
Acceptance Rate 0.99

fig, ax = plt.subplots(nrows=2, sharex=True)
ax[0].plot(params_hmc_logits[:500], label="Trace")
ax[1].plot(torch.sigmoid(params_hmc_logits[:500]), label="Trace")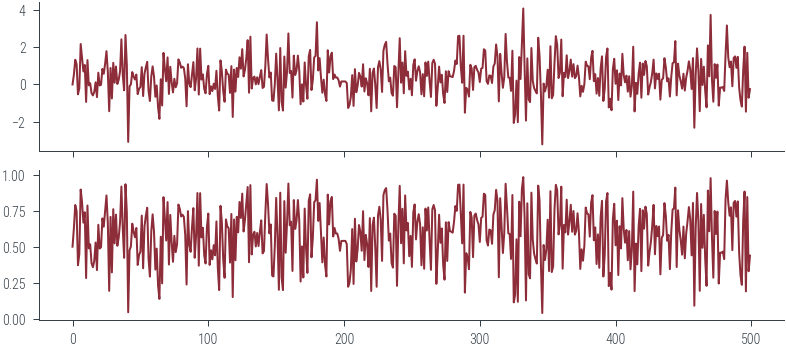

params_hmc_logits[:, 0]

tensor([ 0.0000e+00,  5.2157e-01,  1.3223e+00,  1.0867e+00, -5.2568e-01,
        -2.0241e-01,  2.1629e+00,  1.4570e+00,  6.9446e-01,  1.0426e+00,
        -9.3411e-01,  1.3008e+00, -4.8513e-02,  6.5970e-02, -4.6523e-01,
        -5.8596e-01, -4.0162e-01,  1.1607e-01, -6.7595e-01,  6.2900e-01,
        -5.1382e-02, -1.5011e-02,  8.3155e-01,  5.7020e-01,  1.1027e+00,
         1.7802e+00,  6.8140e-01, -1.4304e+00,  8.8081e-01, -7.4787e-01,
         1.1560e+00,  9.3348e-02,  9.5877e-01,  2.4764e-02,  2.5223e-01,
         7.0275e-01,  2.4133e+00,  5.0036e-01, -3.1154e-01,  2.6437e+00,
         1.0347e+00, -3.0697e+00, -9.9357e-02,  7.0691e-03,  6.6288e-01,
         4.2240e-01,  2.6325e-01,  5.3176e-01, -5.1853e-01, -2.3356e-01,
        -1.3524e-01,  9.2447e-01, -6.1977e-01,  5.7892e-01,  9.1914e-01,
         1.2103e+00, -3.4587e-01, -8.8387e-01,  4.2828e-01,  9.6681e-01,
         4.3113e-01, -6.5857e-01, -5.3167e-02, -1.2148e+00, -1.8391e+00,
         2.7865e-01, -1.1244e+00,  1.6879e+00,  8.4666e-01,  1.7127e-01,
         1.4485e+00, -5.0676e-01,  9.4826e-01,  1.2424e-01, -4.2752e-01,
         3.0383e-01, -1.5217e-01,  6.3599e-02,  1.3415e+00,  1.1742e+00,
         8.9259e-01,  9.5579e-01,  8.8160e-01,  3.3091e-01, -1.1668e+00,
         1.0816e+00,  5.1343e-02, -1.4267e-01,  5.5287e-01,  1.1972e+00,
        -3.1179e-01,  3.0234e-01,  1.9230e+00, -5.4003e-01,  1.9161e+00,
         2.5963e-01,  5.3916e-01, -2.3909e-01, -4.7502e-01,  5.5535e-01,
         9.9362e-01, -5.1886e-01, -1.0049e-01, -3.5520e-01,  4.1397e-02,
        -2.3988e-01,  7.3340e-01, -6.0357e-01, -1.3952e+00,  1.2863e+00,
         6.9414e-01, -3.6833e-01, -9.2557e-01,  7.9619e-01,  5.7926e-01,
         5.2438e-01, -4.5046e-01,  9.7921e-01, -1.7372e+00,  7.9464e-01,
        -3.8177e-01,  8.8204e-01,  4.0353e-01,  1.4525e+00,  8.4391e-01,
         1.8884e+00,  4.2759e-01,  7.8184e-01,  1.4167e+00,  2.3686e+00,
        -4.3994e-01,  2.5539e+00, -2.1615e-01,  3.3379e-01,  4.2178e-01,
         5.1721e-03,  3.8601e-01,  1.7428e-02,  4.2170e-01,  7.6588e-01,
        -1.8764e-01, -1.2382e-01,  9.7327e-01,  2.6694e+00,  1.3677e+00,
         3.7424e-01,  6.3888e-01, -8.4959e-01, -8.8009e-01,  2.3543e-02,
         1.6492e+00,  2.7357e-01, -1.3845e+00,  1.9475e+00, -9.1431e-01,
        -1.3962e+00,  1.4945e+00, -1.6934e-01,  6.8331e-01,  2.7269e+00,
         6.1146e-01,  7.2529e-01, -7.0244e-01,  1.5423e+00,  5.0477e-01,
         7.5417e-01,  1.5440e+00,  7.5432e-01, -1.0567e+00,  6.8278e-03,
        -9.1455e-01,  1.1774e+00, -4.7259e-02, -7.6331e-01,  1.5087e+00,
         1.8454e+00, -2.9682e-01,  2.4198e-01,  1.4402e+00,  1.5362e+00,
         3.3266e+00,  7.4973e-01,  1.4066e+00,  3.8852e-01, -4.4323e-01,
         2.5634e-01, -5.2011e-01, -8.8203e-01,  1.8299e+00,  6.3801e-01,
         1.4932e+00,  1.7013e+00,  2.8509e-01,  5.3203e-01,  3.7003e-01,
         3.6926e-01,  2.1920e-01, -1.1465e-01,  1.6096e-01,  1.6096e-01,
         1.6096e-01,  1.6096e-01,  7.3189e-02, -1.2568e+00, -1.0996e+00,
        -6.6443e-01,  4.9931e-01, -1.1474e+00,  8.1839e-01, -4.1737e-01,
        -7.6412e-02,  6.2048e-01,  4.2288e-01, -1.1374e-01,  1.0812e+00,
        -3.7642e-01,  3.3120e-01,  6.6237e-02, -5.7989e-01,  8.3937e-01,
        -1.4361e+00,  6.1602e-01,  8.5366e-01, -3.5081e-02, -1.2576e+00,
         9.2308e-01,  1.2499e+00,  7.9868e-01, -4.0161e-01,  1.8000e+00,
         2.1205e+00,  2.2769e+00,  1.1112e+00,  1.6897e-01,  3.6750e-01,
        -4.5992e-01, -6.0003e-01,  9.8896e-01,  9.2506e-01, -1.2205e+00,
         6.2656e-01,  2.4740e+00,  9.4190e-02,  1.1711e+00, -4.7227e-01,
         1.7815e+00,  4.5940e-01,  6.8583e-01, -2.6535e-01,  3.0298e-01,
        -5.7829e-01,  1.0377e+00,  1.3456e+00,  2.0190e-01,  7.1908e-01,
         9.7466e-01,  6.5028e-01, -5.2753e-01,  5.5185e-01, -6.3477e-01,
         1.1783e+00,  4.5608e-01,  1.2227e+00,  1.8145e-01, -6.6724e-01,
         1.1463e+00,  1.3225e+00,  1.1086e+00, -1.1422e+00, -1.5377e-01,
         9.5494e-01,  1.0698e-01,  5.1788e-01, -5.0524e-01, -9.8988e-01,
         7.0583e-01, -4.0222e-01,  7.1202e-01,  4.4194e-01,  4.2165e-01,
         3.9502e-01,  7.1842e-01,  1.2794e+00,  1.0915e+00,  2.5821e+00,
         2.6053e+00,  9.5238e-01,  9.0762e-02,  2.6056e+00, -1.5100e+00,
        -1.8069e-01, -2.9206e-01, -6.4654e-01,  1.0541e+00,  8.5845e-01,
        -2.9253e-01,  9.3141e-01,  9.9560e-01,  7.7755e-01,  6.4045e-01,
         1.3102e-01,  8.4557e-01,  8.8637e-01,  1.8827e+00,  1.8122e+00,
         1.7478e-01,  3.1308e-02,  4.8694e-01,  4.5788e-01,  7.9718e-02,
         9.6236e-01,  1.1176e+00,  2.1386e+00,  1.5038e+00, -9.0693e-01,
         1.6350e+00,  6.3332e-01, -1.7795e-01,  3.8162e-01,  2.7007e+00,
         1.2218e+00,  3.7495e-01,  3.5609e-01, -3.4414e-01,  1.8059e+00,
        -2.0574e+00, -1.6110e+00,  2.0561e-01, -2.0184e+00,  1.4640e+00,
         2.9137e-01,  2.2045e+00,  4.0625e+00,  8.4217e-01, -1.9306e+00,
         1.3940e+00, -8.0387e-01, -9.4434e-01,  1.9487e+00,  1.9015e-01,
        -1.9470e-01, -3.5154e-01, -4.7942e-01,  2.4984e+00,  1.5140e+00,
        -5.1064e-01, -3.2031e+00,  4.6453e-02, -3.7326e-01, -7.8675e-02,
         7.8834e-01, -7.0566e-01,  2.0437e+00, -7.3646e-01, -5.6822e-01,
         1.1436e+00,  2.5813e+00,  2.1137e+00,  3.4318e-01,  6.2561e-01,
         2.4020e+00, -6.3089e-01,  6.2534e-01,  4.0191e-01,  1.5595e+00,
         3.4065e-01,  7.1987e-01,  1.3318e+00,  4.2015e-01,  1.0865e+00,
         3.3707e-01,  4.4238e-01,  1.0057e+00,  4.0243e-01, -6.3879e-01,
        -7.3347e-02, -3.9503e-01,  2.3499e-02,  1.2202e+00,  1.0019e+00,
         9.6899e-01,  2.8081e-01,  1.4312e+00,  1.7951e+00,  1.7800e-01,
         5.4844e-01, -4.9231e-01,  3.4481e-01, -6.0484e-01,  8.6655e-01,
         1.5038e+00, -8.8249e-01, -2.3613e-01,  1.4711e+00,  1.9242e+00,
        -1.2292e+00, -7.6492e-01, -1.3766e+00,  8.1369e-01,  1.3737e+00,
         3.7870e-02,  7.5596e-01, -8.3360e-01,  5.8478e-01, -4.8147e-02,
         1.6379e+00,  4.9499e-01,  1.1217e-01,  4.7315e-01, -3.8294e-01,
         4.4057e-01, -6.5282e-01, -6.9137e-02,  2.0160e+00, -1.4416e+00,
         8.7326e-02, -5.0134e-01,  5.9610e-01,  1.1678e+00, -7.0852e-01,
         1.1161e+00,  5.1063e-01,  1.2536e+00,  9.7398e-01, -5.3866e-01,
        -1.5744e-01,  1.3044e-01,  5.9685e-01,  1.3283e+00, -2.1259e-01,
         5.9374e-01,  2.9467e-01,  5.7726e-01, -8.1029e-01,  2.4936e-01,
         3.2499e-01,  1.4028e+00,  9.2111e-01,  1.6626e-01,  3.2936e-01,
        -6.4536e-01,  4.0314e-01,  1.1408e+00,  1.1855e+00,  2.3198e+00,
        -5.8188e-01,  1.1133e+00,  4.7731e-01,  1.7239e-01, -2.2253e-01,
         5.7479e-01, -3.2582e-01,  3.6510e-01,  7.3250e-01,  1.2381e+00,
         7.9945e-01, -2.4175e-01,  1.4102e+00, -2.3131e+00,  5.3915e-01,
         1.9302e+00,  7.3718e-01, -1.4272e+00,  1.3649e+00, -3.0076e-02,
         9.5023e-01, -3.3479e-01, -1.2208e+00,  2.0888e+00,  4.3582e-01,
         3.7189e+00,  2.6196e-01, -9.2166e-01,  1.0887e+00,  3.5772e-01,
         1.0647e+00, -1.1317e+00, -1.6681e-01, -1.6681e-01, -1.3717e-01,
        -3.4850e-01,  1.5862e+00,  3.1538e+00,  1.4352e+00,  9.1958e-01,
         1.2272e+00, -9.4940e-02,  1.4208e+00,  1.4999e+00,  8.8756e-01,
         1.4787e+00, -1.6487e-01, -8.3603e-01, -1.1821e+00,  7.5473e-01,
         2.0233e+00, -1.4535e+00,  1.6937e+00, -7.1143e-01, -2.5059e-01,
         2.3465e-01,  4.7424e-01,  4.7742e-01,  3.3519e-01,  3.3519e-01,
         8.8493e-01,  1.1561e+00, -3.1853e-01, -3.9363e-02,  6.7079e-01,
         5.6049e-01, -5.4034e-01, -2.2138e-01,  2.1434e-01,  1.5668e+00,
        -5.0666e-01,  1.2336e+00,  6.0810e-01,  1.0208e+00, -1.0918e-01,
         6.1068e-01,  3.4561e-01,  3.1687e-01,  1.9952e-01, -4.2316e-01,
        -6.8547e-01,  1.2960e+00,  4.3325e-01, -7.4669e-01,  3.4048e-01,
         5.0448e-01,  1.9143e+00,  3.3597e+00,  7.2327e-01,  7.2327e-01,
         1.9814e+00,  1.7529e+00,  1.2328e+00,  2.3874e+00,  8.9311e-01,
         1.5371e+00,  6.3213e-01, -5.3584e-01,  1.6869e-01,  7.2835e-01,
         5.0431e-01,  1.2030e+00,  1.8420e+00,  3.5781e+00,  2.5207e+00,
         9.1733e-01,  1.2418e+00,  1.0947e+00, -3.2848e-01,  1.4335e+00,
         1.5814e+00,  1.5399e+00,  1.1806e+00,  2.0780e+00,  2.3361e+00,
         7.9356e-02,  1.9177e+00, -2.2122e-01,  2.0555e+00,  1.2023e+00,
         5.6297e-01,  1.7306e+00, -4.2852e-01,  9.2878e-01, -5.6072e-01,
         6.1711e-01,  1.4516e+00,  9.8128e-01,  1.4595e+00,  6.1320e-01,
        -1.5955e+00,  5.4722e-01,  1.9468e+00,  4.5901e-02,  8.8389e-01,
        -3.5987e-01,  1.2097e+00,  6.5788e-01, -6.0313e-01, -3.5547e-01,
         7.2529e-01, -6.0797e-03,  1.8000e+00,  6.2690e-01,  8.4397e-01,
        -5.3849e-01,  1.6233e+00,  1.9809e+00, -3.7226e-01,  1.0213e-01,
         3.9237e-01,  5.6708e-02,  5.8428e-01,  9.4924e-01,  2.1116e+00,
         1.3148e+00, -1.0424e-01, -2.1544e-02,  1.3272e+00,  3.0616e+00,
         9.9475e-01, -1.5997e-01, -5.3483e-01, -5.4581e-01,  1.4050e+00,
         1.8539e+00,  1.6646e+00, -3.4664e-01,  2.1784e-01, -7.7635e-01,
         2.7252e+00, -6.2144e-01, -8.7422e-01,  4.6023e-01, -6.9424e-01,
        -9.1952e-01, -3.1647e-02,  4.7649e-01,  1.8191e+00, -3.3237e-01,
         1.6256e+00,  3.2647e-01,  1.3099e+00,  3.6260e-01,  1.0741e+00,
        -1.5744e-01, -2.6766e-01,  8.3143e-01,  8.5419e-01,  1.2322e+00,
        -1.1485e+00,  3.7815e-01, -2.8660e-01,  1.5768e+00, -3.4889e-01,
         9.6623e-01,  7.0870e-01,  5.1634e-01,  1.2491e+00,  8.7313e-01,
        -4.7971e-01,  3.6604e-01, -4.4042e-01,  6.1318e-02, -1.5561e-01,
        -1.3538e-01, -2.0977e+00, -1.6288e+00,  5.0716e-01, -5.4127e-01,
        -5.1384e-01,  1.0936e+00,  1.3244e+00,  3.1679e-01,  1.6746e+00,
         1.9762e+00,  1.9939e-01,  1.5693e+00,  1.2094e+00,  3.3478e+00,
         1.2666e+00,  2.0992e+00,  2.8287e-02, -4.1169e-01, -6.8056e-01,
         1.0113e+00, -6.9923e-01,  1.6349e+00, -7.5508e-01,  1.5240e+00,
        -4.1570e-01, -4.9153e-02,  3.1265e-01,  2.4256e+00,  9.4421e-01,
         1.2525e-01,  2.6237e-01, -1.7258e-01,  4.4751e-01, -4.6017e-01,
         1.7248e-02,  1.3471e+00, -9.5393e-01,  3.8606e-02,  6.6836e-01,
         7.4823e-01,  7.3605e-01,  2.7526e-02,  1.6556e+00,  1.6328e+00,
         1.8542e+00,  2.4735e+00,  1.0023e+00, -4.9651e-01, -9.9532e-01,
         2.1426e-03, -3.1631e-02, -1.9769e+00, -1.2023e+00,  3.9273e-01,
         3.5130e-01,  1.9974e-02,  1.8765e+00, -1.3989e+00,  1.0675e+00,
         2.0070e-01,  7.1379e-01, -6.7666e-01,  8.5469e-01,  1.8344e-01,
        -3.2166e-01, -3.2166e-01,  1.3211e+00,  4.1828e-01,  1.0699e+00,
         1.5376e+00, -1.7779e-01,  2.8796e-01,  8.1860e-01,  5.8796e-01,
         1.3816e+00,  1.3530e+00,  2.3099e-01,  2.4880e-01,  5.6564e-01,
         1.2632e+00, -1.5422e+00, -1.2768e+00, -5.1313e-01,  7.9212e-01,
         8.6664e-01,  1.8058e-01,  2.4497e-01,  3.2818e-01,  3.7874e-01,
         5.5695e-01, -9.5376e-01,  5.0202e-01, -6.2435e-01,  1.0083e+00,
         2.4775e-01,  1.9974e-01,  1.0435e+00,  1.8181e+00,  1.8181e+00,
         1.5419e+00, -6.8479e-01,  1.0234e+00,  3.4072e-01, -6.8201e-01,
        -6.0094e-03,  5.4767e-01,  1.2085e+00,  1.1278e+00, -2.5554e-01,
        -9.6161e-01, -3.8192e-01,  2.3630e-02,  1.0346e+00, -1.9409e-01,
        -1.7149e-01,  1.2116e+00,  1.0531e+00,  1.7023e-01, -4.3127e-01,
         6.6011e-01,  7.7393e-01, -3.0603e-01,  1.0112e+00,  2.9591e-01,
         1.2036e-01, -4.1267e-01, -4.4962e-01,  7.4402e-01, -6.3659e-01,
         4.6125e-01, -1.3424e+00,  2.4050e-01, -2.0018e-01,  6.3407e-01,
        -2.5910e-01,  9.2403e-02, -3.3480e-01, -3.3480e-01, -6.5366e-01,
         2.5464e-01,  1.3055e+00, -1.5981e+00,  7.8798e-01, -4.1375e-01,
         7.5003e-01,  6.3855e-02, -3.7143e-01,  1.5067e+00,  1.6203e+00,
         5.0651e-01,  1.1662e+00,  6.5912e-01,  6.5912e-01,  9.6239e-01,
        -2.9655e-02, -1.8119e+00,  1.4097e+00,  7.1906e-01,  6.5160e-01,
         6.4548e-01,  8.0345e-01,  1.8066e+00, -1.8827e+00, -1.9057e+00,
         1.7102e-01, -5.2693e-01,  1.8661e-01,  2.8774e-01,  9.7600e-01,
         1.5767e+00,  1.0017e+00,  1.4579e+00, -3.2165e-03,  1.1204e+00,
         1.5134e+00,  2.0321e+00,  1.6208e-01, -7.9307e-01,  1.5747e+00,
         7.5000e-01, -3.5063e-03,  2.1710e+00,  9.3272e-01, -3.8879e-04,
         1.1818e+00, -1.7795e-02, -2.4369e-01, -1.9889e+00, -5.1913e-01,
        -7.0746e-01,  1.6388e+00,  1.4992e+00,  1.7651e+00,  3.5630e+00,
         4.6029e-02, -1.4069e+00,  5.9076e-02,  2.2806e+00, -8.9770e-01,
        -6.2536e-01,  1.6230e+00,  1.5135e+00,  7.6925e-01, -3.8131e-01,
         1.7301e+00,  1.3660e+00,  6.2360e-01,  5.6905e-01, -3.4309e-01,
        -1.1920e+00,  1.8200e+00, -5.0699e-01,  4.0612e-02,  1.2228e+00,
         9.6594e-01, -7.0298e-01, -6.2520e-01,  1.6632e+00,  8.8678e-01,
         5.2583e-01,  9.1454e-01,  1.4418e+00,  1.4364e+00,  5.6974e-01,
        -1.1927e+00,  4.6645e-01,  5.5446e-01,  7.2413e-01,  1.9243e+00,
         7.7880e-01, -7.4584e-01,  1.2390e+00, -1.1413e-01,  1.2299e+00,
         1.0727e+00, -2.9502e-01,  3.1766e-01,  3.7765e-01,  9.4944e-01,
        -2.1452e-01, -4.7935e-01,  1.0967e+00, -2.7905e-01, -8.6457e-01,
         1.1860e+00, -1.1904e+00,  5.9031e-01,  6.6663e-01,  1.2639e+00,
         6.7896e-02, -1.0120e+00,  2.5375e+00,  1.8990e+00, -1.0375e+00,
         4.4640e-01,  1.4028e+00,  1.1473e+00,  6.1459e-01,  3.9804e-01,
         7.8219e-01,  1.6068e+00,  5.6333e-01,  1.6903e-01, -8.0579e-01,
        -7.3818e-01,  1.0135e+00,  1.1724e+00, -3.5863e-01, -3.4891e-01,
        -2.9014e-01,  1.9020e+00,  1.0430e+00,  2.6433e+00,  3.1035e+00,
         2.0789e+00, -4.8755e-01, -1.5892e+00, -1.9662e+00,  1.1934e+00,
         1.1145e+00, -7.9593e-02,  1.2906e+00,  3.1053e-01, -5.8267e-01,
         1.4457e+00,  7.9235e-01,  9.0271e-01,  4.6118e-01,  1.0147e+00,
         2.2204e+00,  1.0090e+00,  2.4175e-01, -6.5125e-01,  5.9952e-01,
         2.0044e+00,  8.9869e-01, -2.2489e-01, -1.0497e+00,  2.0135e+00,
        -4.7356e-01,  4.7832e-01, -1.2162e-01,  1.1530e+00, -1.1612e-02,
         1.4690e+00,  1.0307e+00,  2.2840e+00,  3.3513e+00,  8.8326e-01,
         1.2590e+00,  1.7236e+00,  4.5989e-01,  6.4716e-01,  3.0418e-01,
         3.9410e-01,  3.4654e-01,  1.4171e+00,  6.6960e-01,  6.7712e-01,
        -2.0732e-01, -1.0382e-01,  9.9374e-01,  1.6327e+00,  3.1100e-01,
         4.4393e-01, -2.9965e-01,  1.9955e-01, -9.0940e-03,  6.6451e-02,
         1.8670e+00,  1.3433e+00, -1.4861e+00, -1.5094e+00,  1.1104e+00,
        -4.7540e-02,  8.7289e-01, -8.7741e-01,  1.6113e+00, -2.0599e-01,
         2.9714e-01,  2.4836e+00,  8.8014e-01,  2.2057e+00,  1.5712e+00,
         6.9619e-02,  2.8588e-02, -3.6439e-01,  7.4889e-01,  9.1645e-01])

# Plot posterior KDE using seaborn but clip to [0, 1]
sns.kdeplot(
    torch.sigmoid(params_hmc_logits[:, 0]).detach().numpy(),
    label="Samples",
    shade=True,
    color="C1",
    clip=(0, 1),
)
# True posterior
x_lin = torch.linspace(0, 1, 1000)
y_lin = dist.Beta(1 + 3, 1 + 2).log_prob(x_lin).exp()
plt.plot(x_lin, y_lin, label="True posterior")
plt.legend()

<matplotlib.legend.Legend at 0x7fb3376f4ac0>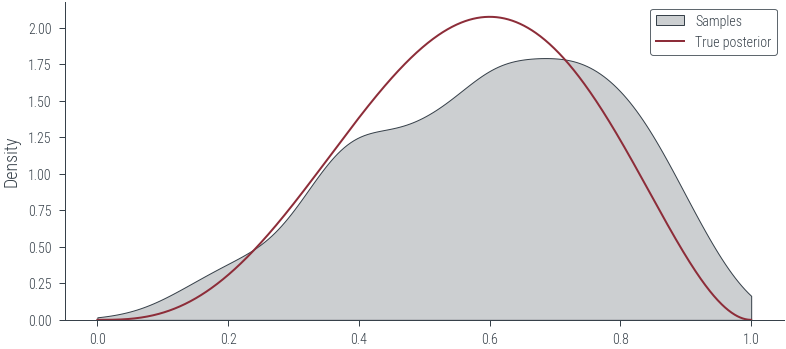

# Linear regression for 1 dimensional input using HMC

torch.manual_seed(123)
x_lin = torch.linspace(-3, 3, 90)
theta_0_true = torch.tensor([2.0])
theta_1_true = torch.tensor([3.0])
f = lambda x: theta_0_true + theta_1_true * x
eps = torch.randn_like(x_lin) * 1.0
y_lin = f(x_lin) + eps

plt.scatter(x_lin, y_lin, label="Data", color="C0")
plt.plot(x_lin, f(x_lin), label="Ground truth")
plt.xlabel("x")
plt.ylabel("y")

Text(0, 0.5, 'y')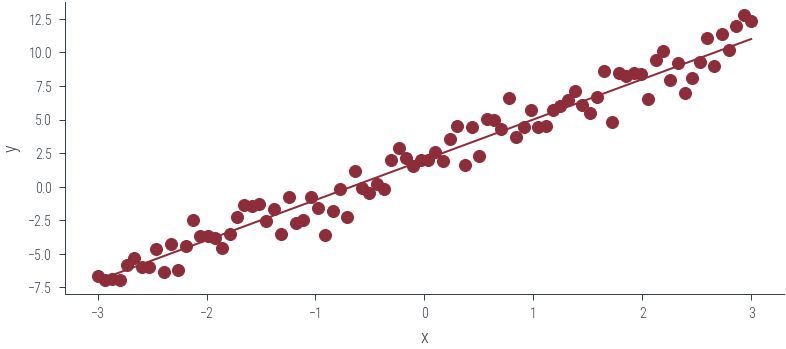

# Esimate theta_0, theta_1 using HMC assuming noise variance is known to be 1
def logprob(theta):
    y_pred = theta[0] + x_lin * theta[1]
    # print(y_pred.shape, y_lin.shape)
    # print(y_pred.shape, y_lin.shape, y_pred)
    return dist.Normal(y_pred, 1).log_prob(y_lin).sum()


def log_prior(theta):
    return dist.Normal(0, 1).log_prob(theta).sum()


def log_posterior(theta):
    log_prior_val = log_prior(theta)
    log_likelihood = logprob(theta)
    log_joint = log_prior_val + log_likelihood
    # print(log_joint, log_prior_val, log_likelihood)
    return log_joint

params = torch.tensor([0.1, 0.2])
print(params.dtype)
params_hmc_lin_reg = run_hmc(log_posterior, params, 1000, 0.1, 5)

torch.float32
Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:03 | 0d:00:00:00 | #################### | 1000/1000 | 265.17       
Acceptance Rate 0.83

Sampling (Sampler.HMC; Integrator.IMPLICIT) Time spent | Time remain.| Progress | Samples | Samples/sec tensor(-1433.3967, grad_fn=) tensor(-1.8629, grad_fn=) tensor(-1431.5338, grad_fn=) tensor(-1433.3967, grad_fn=) tensor(-1.8629, grad_fn=) tensor(-1431.5338, grad_fn=) tensor(-355.0762, grad_fn=) tensor(-10.8475, grad_fn=) tensor(-344.2287, grad_fn=) tensor(-729.5259, grad_fn=) tensor(-18.6343, grad_fn=) tensor(-710.8916, grad_fn=) tensor(-1269.0886, grad_fn=) tensor(-9.7863, grad_fn=) tensor(-1259.3024, grad_fn=) tensor(-218.4335, grad_fn=) tensor(-12.0944, grad_fn=) tensor(-206.3391, grad_fn=) tensor(-1101.4713, grad_fn=) tensor(-19.0104, grad_fn=) tensor(-1082.4608, grad_fn=) tensor(-1101.4713, grad_fn=) tensor(-19.0104, grad_fn=) tensor(-1082.4608, grad_fn=) 0d:00:00:00 | 0d:00:00:00 | #################### | 1/1 | 140.03
Acceptance Rate 1.00

params_hmc_lin_reg

tensor([[0.1000, 0.2000],
        [1.7248, 0.6831],
        [2.1176, 5.2166],
        ...,
        [1.9162, 3.1325],
        [2.1559, 2.9292],
        [1.8733, 3.0645]])

# Plot the traces corresponding to the two parameters
fig, axes = plt.subplots(2, 1, sharex=True)

for i, param_vals in enumerate(params_hmc_lin_reg.T):
    axes[i].plot(param_vals, label="Trace")
    axes[i].set_xlabel("Iteration")
    axes[i].set_ylabel(rf"$\theta_{i}$")

# Plot the true values as well
for i, param_vals in enumerate([theta_0_true, theta_1_true]):
    axes[i].axhline(param_vals.numpy(), color="C1", label="Ground truth")
    axes[i].legend()

findfont: Font family ['cursive'] not found. Falling back to DejaVu Sans.
findfont: Generic family 'cursive' not found because none of the following families were found: Apple Chancery, Textile, Zapf Chancery, Sand, Script MT, Felipa, Comic Neue, Comic Sans MS, cursive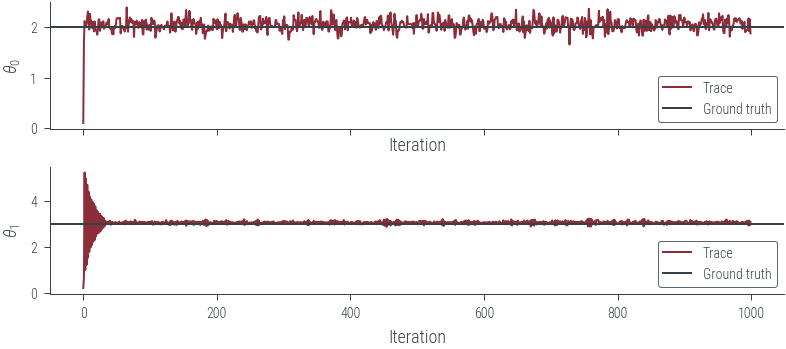

# Plot KDE of the samples for the two parameters
fig, axes = plt.subplots(2, 1, sharex=True)

for i, param_vals in enumerate(params_hmc_lin_reg.T):
    sns.kdeplot(
        param_vals.detach().numpy(), label="Samples", shade=True, color="C1", ax=axes[i]
    )
    axes[i].set_ylabel(rf"$\theta_{i}$")

# Plot the true values as well
for i, param_vals in enumerate([theta_0_true, theta_1_true]):
    axes[i].axvline(param_vals.numpy(), color="C0", label="Ground truth")
    axes[i].legend()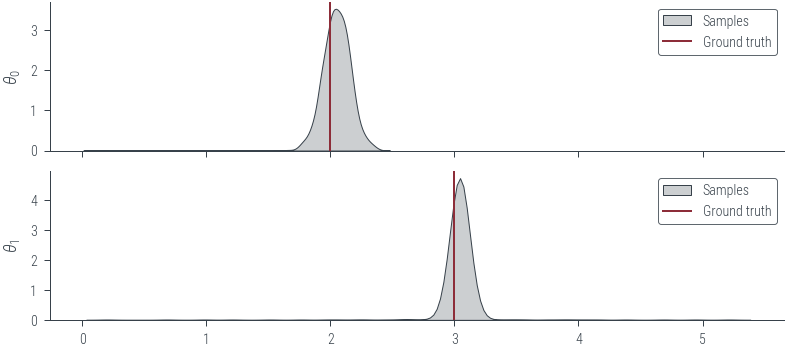

# Plot the posterior predictive distribution
plt.figure()
plt.scatter(x_lin, y_lin, label="Data", color="C0")
plt.plot(x_lin, f(x_lin), label="Ground truth", color="C1", linestyle="--")
plt.xlabel("x")
plt.ylabel("y")

# Get posterior samples. Thin first 100 samples to remove burn-in
posterior_samples = params_hmc_lin_reg[100:].detach()
y_hat = posterior_samples[:, 0].unsqueeze(1) + x_lin * posterior_samples[
    :, 1
].unsqueeze(1)

# Plot mean and 95% confidence interval

plt.plot(x_lin, y_hat.mean(axis=0), label="Mean", color="C2")
plt.fill_between(
    x_lin,
    y_hat.mean(axis=0) - 2 * y_hat.std(axis=0),
    y_hat.mean(axis=0) + 2 * y_hat.std(axis=0),
    alpha=0.5,
    label="95% CI",
    color="C2",
)
plt.legend()

<matplotlib.legend.Legend at 0x7fb336ba0d30>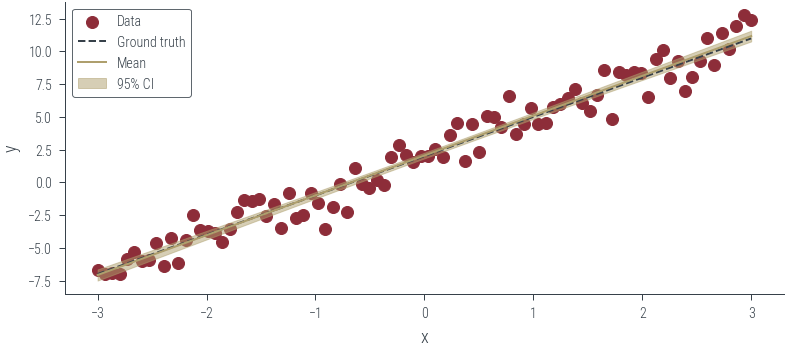

# Using a neural network with HMC


class Net(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = torch.nn.Linear(1, 1)

    def forward(self, x):
        x = self.fc1(x)
        return x

net = Net()
net

Net(
  (fc1): Linear(in_features=1, out_features=1, bias=True)
)

hamiltorch.util.flatten(net).shape

torch.Size([2])

theta_params = hamiltorch.util.flatten(net)
theta_params.shape

torch.Size([2])

params_list = hamiltorch.util.unflatten(net, theta_params)
params_list[0].shape, params_list[1].shape

(torch.Size([1, 1]), torch.Size([1]))

params_init = theta_params.clone().detach()
params_init.dtype

torch.float32

t = torch.tensor([0.1, 0.2])
# reverse t
t.flip(0)

tensor([0.2000, 0.1000])

# hamiltorch.util.update_model_params_in_place??

theta = torch.tensor([0.1, 0.2])
print(theta.shape)
params_list = hamiltorch.util.unflatten(net, theta)
print(params_list, params_list[0].shape, params_list[1].shape)
hamiltorch.util.update_model_params_in_place(net, params_list)
net.state_dict()
net(torch.tensor([[1.0]]))

torch.Size([2])
[tensor([[0.1000]]), tensor([0.2000])] torch.Size([1, 1]) torch.Size([1])

tensor([[0.3000]], grad_fn=<AddmmBackward0>)

def log_prior(theta):
    return dist.Normal(0, 1).log_prob(theta).sum()


def log_likelihood(theta):
    theta = theta.flip(0)
    params_list = hamiltorch.util.unflatten(net, theta)

    ### Inplace call
    # hamiltorch.util.update_model_params_in_place(net, params_list)
    # y_pred = net(x_lin.unsqueeze(1)).squeeze()
    # print(y_pred[0:4], "first")

    ## Functional call
    params = net.state_dict()
    for i, (name, _) in enumerate(params.items()):
        params[name] = params_list[i]
    y_pred = torch.func.functional_call(net, params, x_lin.unsqueeze(1)).squeeze()
    # print(y_pred[0:4], "second")

    # print(y_pred.shape, y_lin.shape, y_pred)
    return dist.Normal(y_pred, 1).log_prob(y_lin).sum()


def log_joint(theta):
    log_prior_val = log_prior(theta)
    log_likelihood_val = log_likelihood(theta)
    log_joint = log_prior_val + log_likelihood_val
    # print(log_joint, log_prior_val, log_likelihood_val)
    return log_joint


params_hmc = run_hmc(log_joint, torch.tensor([0.1, 0.2]), 1000, 0.1, 5)
params_hmc

Sampling (Sampler.HMC; Integrator.IMPLICIT)
Time spent  | Time remain.| Progress             | Samples   | Samples/sec
0d:00:00:04 | 0d:00:00:00 | #################### | 1000/1000 | 201.06       
Acceptance Rate 0.81

tensor([[0.1000, 0.2000],
        [1.6531, 0.5802],
        [2.0851, 5.3383],
        ...,
        [1.9668, 3.0019],
        [2.0264, 3.0395],
        [2.0264, 3.0395]])

# Plot the traces corresponding to the two parameters
fig, axes = plt.subplots(2, 1, sharex=True)

for i, param_vals in enumerate(params_hmc.T):
    axes[i].plot(param_vals, label="Trace")
    axes[i].set_xlabel("Iteration")
    axes[i].set_ylabel(rf"$\theta_{i}$")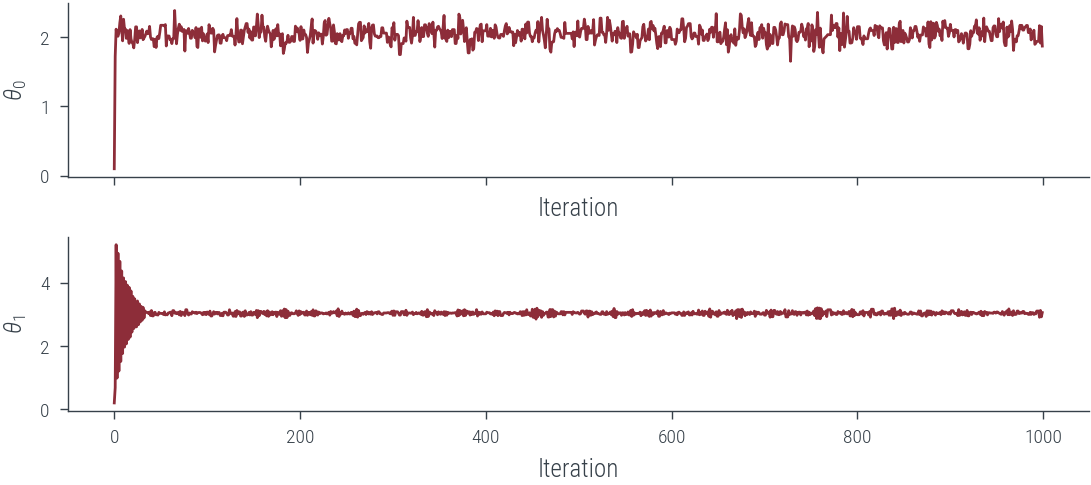

# Plot KDE of the samples for the two parameters
fig, axes = plt.subplots(2, 1, sharex=True)

for i, param_vals in enumerate(params_hmc.T):
    sns.kdeplot(
        param_vals.detach().numpy(), label="Samples", shade=True, color="C1", ax=axes[i]
    )
    axes[i].set_ylabel(rf"$\theta_{i}$")

NameError: name 'sns' is not defined

# Plot predictions
plt.figure()
plt.scatter(x_lin, y_lin, label="Data", color="C0")
plt.plot(x_lin, f(x_lin), label="Ground truth", color="C1", linestyle="--")
plt.xlabel("x")
plt.ylabel("y")

# Get posterior samples. Thin first 100 samples to remove burn-in
posterior_samples = params_hmc[100:].detach()
with torch.no_grad():
    y_hat = net(x_lin.unsqueeze(1))

# Plot mean and 95% confidence interval

plt.plot(x_lin, y_hat.ravel(), label="Mean", color="C2")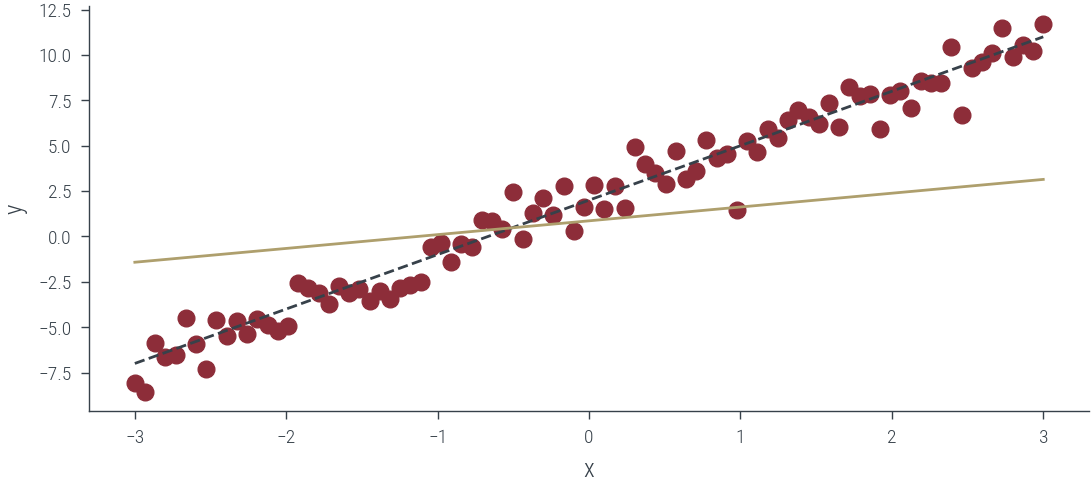

y_hat.ravel()

tensor([-1.4220, -1.3707, -1.3194, -1.2681, -1.2168, -1.1656, -1.1143, -1.0630,
        -1.0117, -0.9604, -0.9091, -0.8579, -0.8066, -0.7553, -0.7040, -0.6527,
        -0.6014, -0.5501, -0.4989, -0.4476, -0.3963, -0.3450, -0.2937, -0.2424,
        -0.1912, -0.1399, -0.0886, -0.0373,  0.0140,  0.0653,  0.1165,  0.1678,
         0.2191,  0.2704,  0.3217,  0.3730,  0.4242,  0.4755,  0.5268,  0.5781,
         0.6294,  0.6807,  0.7320,  0.7832,  0.8345,  0.8858,  0.9371,  0.9884,
         1.0397,  1.0909,  1.1422,  1.1935,  1.2448,  1.2961,  1.3474,  1.3986,
         1.4499,  1.5012,  1.5525,  1.6038,  1.6551,  1.7064,  1.7576,  1.8089,
         1.8602,  1.9115,  1.9628,  2.0141,  2.0653,  2.1166,  2.1679,  2.2192,
         2.2705,  2.3218,  2.3730,  2.4243,  2.4756,  2.5269,  2.5782,  2.6295,
         2.6808,  2.7320,  2.7833,  2.8346,  2.8859,  2.9372,  2.9885,  3.0397,
         3.0910,  3.1423])

# Now, solve the above using Hamiltorch's MCMC sample_model function

### Bayesian Logistic Regression

from sklearn.datasets import make_moons

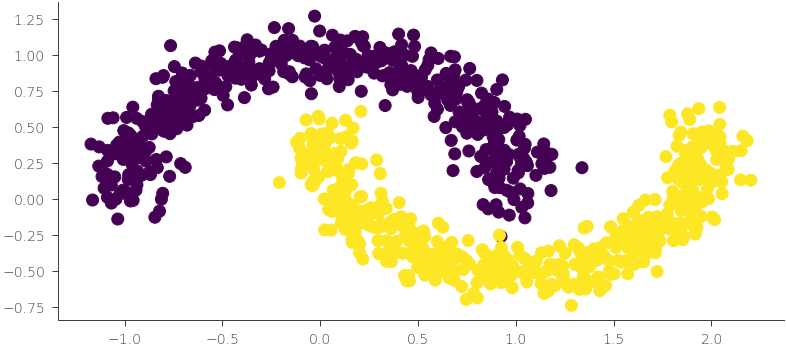
# Generate data
x, y = make_moons(n_samples=1000, noise=0.1, random_state=0)

plt.scatter(x[:, 0], x[:, 1], c=y)

x = torch.tensor(x).float()
y = torch.tensor(y).float()