CIFAR10 and CIFAR100 dataset

https://www.cs.toronto.edu/~kriz/cifar.html

Ref: https://hjweide.github.io/quantifying-uncertainty-in-neural-networks

1. Red objects: cars or apples?
2. Green objects: frogs? or apples?

Reference slides

https://classifier-calibration.github.io/assets/slides/clacal_tutorial_ecmlpkdd_2020_intro.pdf

First 7 slides from above link

import torch
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# Retina display
%config InlineBackend.figure_format = 'retina'

from tueplots import bundles
plt.rcParams.update(bundles.beamer_moml())


# Also add despine to the bundle using rcParams
plt.rcParams['axes.spines.right'] = False
plt.rcParams['axes.spines.top'] = False

# Increase font size to match Beamer template
plt.rcParams['font.size'] = 16
# Make background transparent
plt.rcParams['figure.facecolor'] = 'none'

from sklearn.datasets import make_moons
from sklearn.linear_model import LogisticRegression

X, y = make_moons(n_samples=1000, noise=0.1, random_state=0)

clf = LogisticRegression()

clf.fit(X, y)

LogisticRegression()

p_hats = clf.predict_proba(X)[:, 1]
p_hats[:10]

array([0.60804417, 0.96671272, 0.02867904, 0.41138351, 0.9631718 ,
       0.72298419, 0.51086972, 0.0148838 , 0.01696895, 0.98714042])

true_labels = y
true_labels[:10]

array([1, 1, 0, 1, 1, 1, 0, 0, 0, 1])

df = pd.DataFrame({'p_hat': p_hats, 'y': true_labels})
df.head()

	p_hat	y
0	0.608044	1
1	0.966713	1
2	0.028679	0
3	0.411384	1
4	0.963172	1

# Let us look at samples where p_hat is close to 0.5 (say between 0.45 and 0.55)
df_close_phat_val = df[(df.p_hat > 0.45) & (df.p_hat < 0.55)]
df_close_phat_val.head()

	p_hat	y
6	0.510870	0
15	0.481702	0
20	0.533697	0
41	0.522857	1
60	0.483962	1

len(df_close_phat_val)

31

# Histogram of p_hat values
df.p_hat.hist(bins=50)
plt.xlabel('$\hat{p}$')
plt.ylabel('Frequency')
plt.title('Histogram of $\hat{p}$ values');

findfont: Font family ['cursive'] not found. Falling back to DejaVu Sans.
findfont: Generic family 'cursive' not found because none of the following families were found: Apple Chancery, Textile, Zapf Chancery, Sand, Script MT, Felipa, Comic Neue, Comic Sans MS, cursive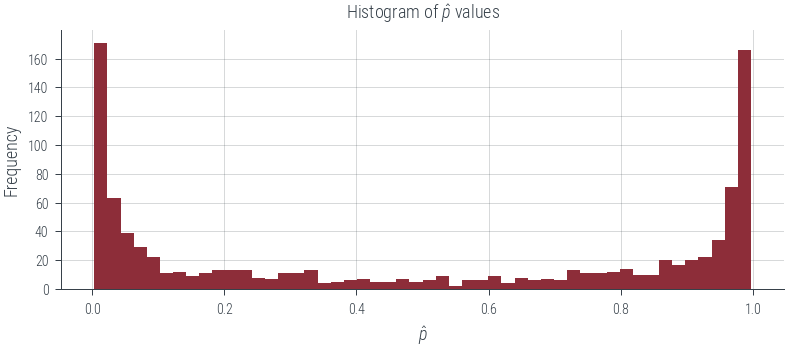

# Out of these len(df_close_phat_val) samples, how many are actually positive? 

df_close_phat_val.y.sum()

18

# Fraction of positive samples
df_close_phat_val.y.sum() / len(df_close_phat_val)

0.5806451612903226

# This is the reliability of the classifier at p_hat = 0.5

bins = np.linspace(0, 1, 11)
bins

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])

# Let us add a column to the dataframe that tells us which bin each sample belongs to

df['bin'] = pd.cut(df.p_hat, bins=bins)
df.head()

	p_hat	y	bin
0	0.608044	1	(0.6, 0.7]
1	0.966713	1	(0.9, 1.0]
2	0.028679	0	(0.0, 0.1]
3	0.411384	1	(0.4, 0.5]
4	0.963172	1	(0.9, 1.0]

# Let us compute the reliability of the classifier in each bin

df.groupby('bin').y.mean()

bin
(0.0, 0.1]    0.006231
(0.1, 0.2]    0.241379
(0.2, 0.3]    0.269231
(0.3, 0.4]    0.375000
(0.4, 0.5]    0.620690
(0.5, 0.6]    0.413793
(0.6, 0.7]    0.529412
(0.7, 0.8]    0.722222
(0.8, 0.9]    0.849315
(0.9, 1.0]    0.987097
Name: y, dtype: float64

# Calculate the reliability diagram points
mean_predicted_probs = df.groupby('bin').p_hat.mean()
fraction_of_positives = df.groupby('bin').y.mean()

bin_sizes = df.groupby('bin').size()
bin_sizes

bin
(0.0, 0.1]    321
(0.1, 0.2]     58
(0.2, 0.3]     52
(0.3, 0.4]     40
(0.4, 0.5]     29
(0.5, 0.6]     29
(0.6, 0.7]     34
(0.7, 0.8]     54
(0.8, 0.9]     73
(0.9, 1.0]    310
dtype: int64

ece = (np.abs(mean_predicted_probs - fraction_of_positives) * bin_sizes / len(df)).sum()
ece

0.036133146181597894

plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k:')
plt.plot(mean_predicted_probs, fraction_of_positives, 'o-')
plt.xlabel('Predicted probability')
plt.ylabel('Fraction of positives')
plt.title(f'Reliability Diagram (ECE={ece:.4f})')
plt.gca().set_aspect('equal')

# Plot the bar also
plt.bar(mean_predicted_probs, fraction_of_positives, width=0.1, alpha=0.1)

<BarContainer object of 10 artists>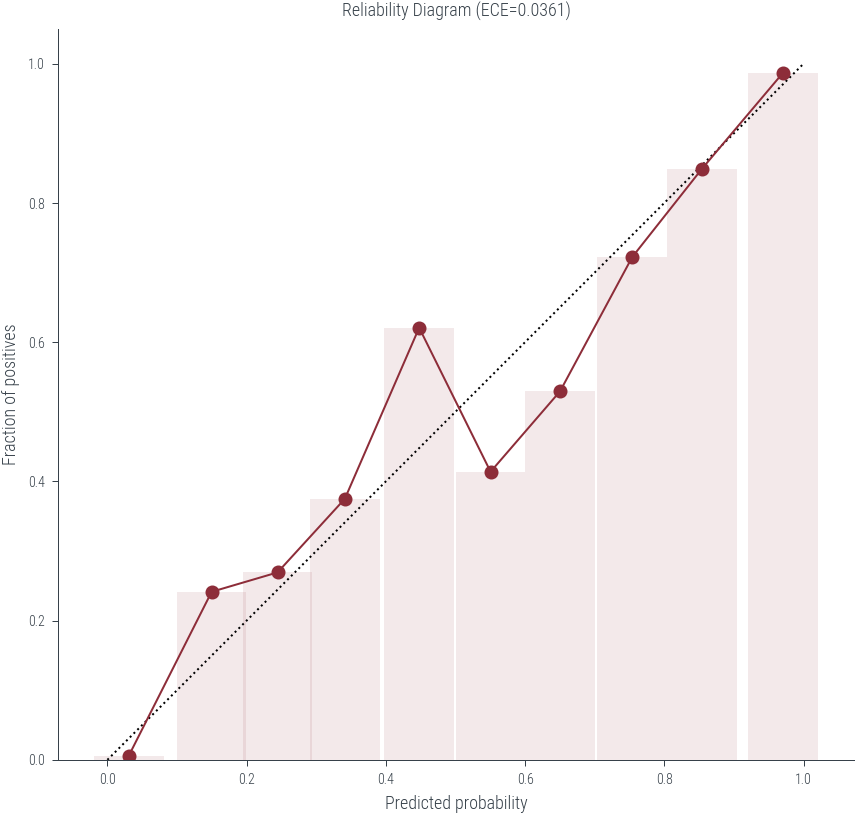

from sklearn.calibration import calibration_curve

prob_true, prob_pred = calibration_curve(df['y'], df['p_hat'], n_bins=10, strategy='uniform')

assert np.allclose(prob_true, fraction_of_positives)

assert np.allclose(prob_pred, mean_predicted_probs)

pd.DataFrame({'prob_true': prob_true, 'prob_pred': prob_pred})

	prob_true	prob_pred
0	0.006231	0.030912
1	0.241379	0.149753
2	0.269231	0.244433
3	0.375000	0.341098
4	0.620690	0.447832
5	0.413793	0.550410
6	0.529412	0.650223
7	0.722222	0.753892
8	0.849315	0.854304
9	0.987097	0.970665

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.calibration import calibration_curve

def plot_reliability_diagram(classifier, X, y, n_bins=10, ax=None):
    """
    Generate a reliability diagram and calculate ECE for a classifier.

    Parameters:
    - classifier: A scikit-learn classifier with a `predict_proba` method.
    - X: Input features for the dataset.
    - y: True labels for the dataset.
    - n_bins: Number of bins for the reliability diagram.
    - ax: Matplotlib axes object to plot on.

    Returns:
    - ece: Expected Calibration Error (ECE).
    """
    if ax is None:
        fig, ax = plt.subplots()

    # Fit the classifier
    classifier.fit(X, y)

    # Predict probabilities
    p_hats = classifier.predict_proba(X)[:, 1]

    # Create a DataFrame
    df = pd.DataFrame({'p_hat': p_hats, 'y': y})

    # Create bins based on predicted probabilities
    bins = np.linspace(0, 1, n_bins + 1)
    df['bin'] = pd.cut(df['p_hat'], bins=bins)
    
    mean_predicted_probs = df.groupby('bin').p_hat.mean()
    fraction_of_positives = df.groupby('bin').y.mean()
    
    # Fill NANs with 0
    mean_predicted_probs = mean_predicted_probs.fillna(0)
    fraction_of_positives = fraction_of_positives.fillna(0)

    # Calculate the Expected Calibration Error (ECE) weighted by bin sizes
    bin_sizes = df.groupby('bin').size()
    
    # Ensure bin_sizes align with prob_true and prob_pred
    #bin_sizes = bin_sizes.reindex(range(n_bins), fill_value=0)
    #return bin_sizes, mean_predicted_probs, fraction_of_positives

    ece = (np.abs(mean_predicted_probs - fraction_of_positives) * bin_sizes / bin_sizes.sum()).sum()

    # Create the reliability diagram plot
    #plt.figure(figsize=(6, 6))
    ax.plot([0, 1], [0, 1], 'k:')
    ax.scatter(mean_predicted_probs, fraction_of_positives)
    # Plot bar also
    ax.bar(mean_predicted_probs, fraction_of_positives, width=0.1, alpha=0.1)
    ax.set_xlabel('Mean Predicted Probability')
    ax.set_ylabel('Fraction of Positives')
    ax.set_title(f'Calibration Curve (ECE={ece:.4f})')
    #plt.gca().set_aspect('equal')
    return ece

from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.calibration import CalibrationDisplay

# Generate the dataset
X, y = make_moons(n_samples=1000, noise=0.1, random_state=0)

# List of classifiers to evaluate
classifiers = [
    ('Logistic Regression', LogisticRegression()),
    ('Random Forest', RandomForestClassifier(n_estimators=100, random_state=0)),
    ('Support Vector Classifier', SVC(probability=True)),
    ('K-Nearest Neighbors', KNeighborsClassifier(n_neighbors=3))
]

fig, axarr = plt.subplots(figsize=(6, 6), nrows=len(classifiers), ncols=2)

# Loop through the classifiers and generate reliability diagrams
for i, (name, classifier) in enumerate(classifiers):
    ece = plot_reliability_diagram(classifier, X, y, ax=axarr[i, 0])
    print(f"Classifier: {name}")
    print(f"ECE: {ece:.4f}")


    
    CalibrationDisplay.from_estimator(
        classifier,
        X,
        y,
        n_bins=10,
        ax = axarr[i, 1],
        name=name
    )
    print("*"*20)
    print("*"*20)
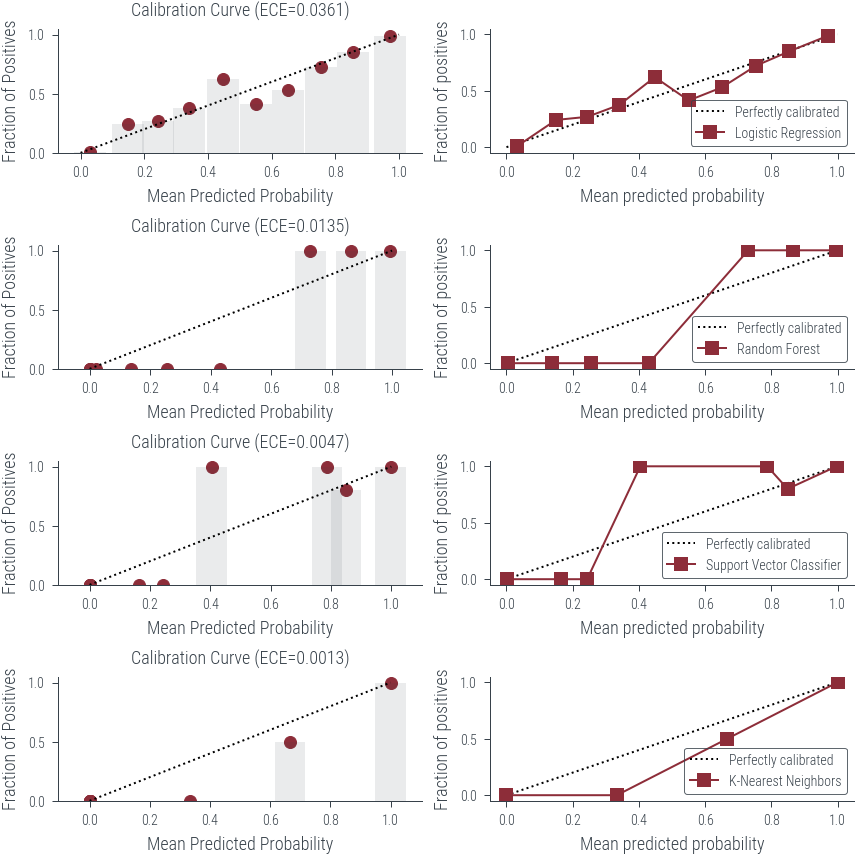
    print("\n" + "=" * 50 + "\n")

Classifier: Logistic Regression
ECE: 0.0361
********************
********************

==================================================

Classifier: Random Forest
ECE: 0.0135
********************
********************

==================================================

Classifier: Support Vector Classifier
ECE: 0.0047
********************
********************

==================================================

Classifier: K-Nearest Neighbors
ECE: 0.0013
********************
********************

==================================================

Multiclass reliability diagram

Slide 26 from https://classifier-calibration.github.io/assets/slides/clacal_tutorial_ecmlpkdd_2020_intro.pdf

# Now, multi-class classification and reliability diagrams

from sklearn.datasets import make_classification, make_blobs

X, y = make_blobs(n_samples=1000, centers=3, n_features=2, random_state=0)

# Plot the dataset
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')

<matplotlib.collections.PathCollection at 0x7f33e5367eb0>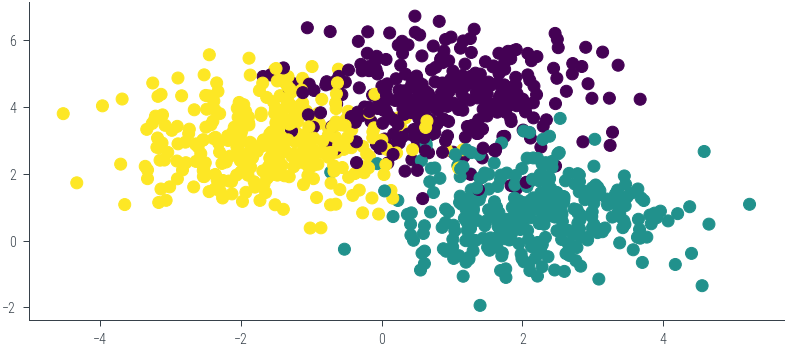

clf = LogisticRegression()
clf.fit(X, y)

LogisticRegression()

preds = pd.DataFrame(clf.predict_proba(X))

preds

	0	1	2
0	0.068741	0.005454	0.925805
1	0.983384	0.015859	0.000757
2	0.021072	0.000240	0.978688
3	0.042703	0.001372	0.955925
4	0.000208	0.000026	0.999766
...	...	...	...
995	0.005001	0.994489	0.000510
996	0.050768	0.015765	0.933467
997	0.006151	0.911409	0.082440
998	0.000271	0.000021	0.999708
999	0.021539	0.962650	0.015811

1000 rows × 3 columns

preds['y'] = y

preds.head(10)

	0	1	2	y
0	0.068741	0.005454	0.925805	2
1	0.983384	0.015859	0.000757	0
2	0.021072	0.000240	0.978688	2
3	0.042703	0.001372	0.955925	2
4	0.000208	0.000026	0.999766	2
5	0.179771	0.797045	0.023183	1
6	0.120874	0.003821	0.875305	0
7	0.957242	0.000002	0.042756	0
8	0.000908	0.998876	0.000216	1
9	0.836772	0.162509	0.000718	0

# Syntax highlighting to show highest amongst the three columns
most_probable_class = preds[[0, 1, 2]].idxmax(axis=1)

# Add the most probable class to the DataFrame
preds['y_hat'] = most_probable_class

preds.head()

	0	1	2	y	y_hat
0	0.068741	0.005454	0.925805	2	2
1	0.983384	0.015859	0.000757	0	0
2	0.021072	0.000240	0.978688	2	2
3	0.042703	0.001372	0.955925	2	2
4	0.000208	0.000026	0.999766	2	2

# Let us simplify dataframe to only include the most probable class probability and whether the prediction was correct or not
new_df = preds.copy()
new_df["Correct"] = new_df.y == new_df.y_hat
new_df["Most_Probable_Class_Probability"] = new_df[[0, 1, 2]].max(axis=1)

new_df.head()

	0	1	2	y	y_hat	Correct	Most_Probable_Class_Probability
0	0.068741	0.005454	0.925805	2	2	True	0.925805
1	0.983384	0.015859	0.000757	0	0	True	0.983384
2	0.021072	0.000240	0.978688	2	2	True	0.978688
3	0.042703	0.001372	0.955925	2	2	True	0.955925
4	0.000208	0.000026	0.999766	2	2	True	0.999766

# drop the other columns
new_df = new_df.drop(columns=[0, 1, 2, 'y', 'y_hat'])
new_df.head()

	Correct	Most_Probable_Class_Probability
0	True	0.925805
1	True	0.983384
2	True	0.978688
3	True	0.955925
4	True	0.999766

# Let us look at samples where the most probable class probability is close to 0.5 (say between 0.45 and 0.55)
df_close_phat_val = new_df[(new_df.Most_Probable_Class_Probability > 0.45) & (new_df.Most_Probable_Class_Probability < 0.55)]
df_close_phat_val.head()

	Correct	Most_Probable_Class_Probability
27	True	0.532492
127	False	0.537886
135	True	0.536489
171	True	0.512435
203	False	0.534704

df_close_phat_val.Correct.sum() / len(df_close_phat_val)

0.4838709677419355

# Now, let us compute the reliability of the classifier in each bin
bins = np.linspace(0, 1, 11)

# Cuts the data by the bins
new_df['bin'] = pd.cut(new_df.Most_Probable_Class_Probability, bins=bins)

new_df.head(10)

	Correct	Most_Probable_Class_Probability	bin
0	True	0.925805	(0.9, 1.0]
1	True	0.983384	(0.9, 1.0]
2	True	0.978688	(0.9, 1.0]
3	True	0.955925	(0.9, 1.0]
4	True	0.999766	(0.9, 1.0]
5	True	0.797045	(0.7, 0.8]
6	False	0.875305	(0.8, 0.9]
7	True	0.957242	(0.9, 1.0]
8	True	0.998876	(0.9, 1.0]
9	True	0.836772	(0.8, 0.9]

# Calculate the reliability diagram points
mean_predicted_probs = new_df.groupby('bin').Most_Probable_Class_Probability.mean()
fraction_of_positives = new_df.groupby('bin').Correct.mean()

bin_sizes = new_df.groupby('bin').size()

ece = (np.abs(mean_predicted_probs - fraction_of_positives) * bin_sizes / len(new_df)).sum()

ece

0.016551445751129316

# Plot the reliability diagram
plt.figure(figsize=(6, 6))
plt.plot([0, 1], [0, 1], 'k:')
plt.plot(mean_predicted_probs, fraction_of_positives, 'o-')
plt.xlabel('Predicted probability')
plt.ylabel('Fraction of positives')
plt.title(f'Reliability Diagram (ECE={ece:.4f})')

Text(0.5, 1.0, 'Reliability Diagram (ECE=0.0166)')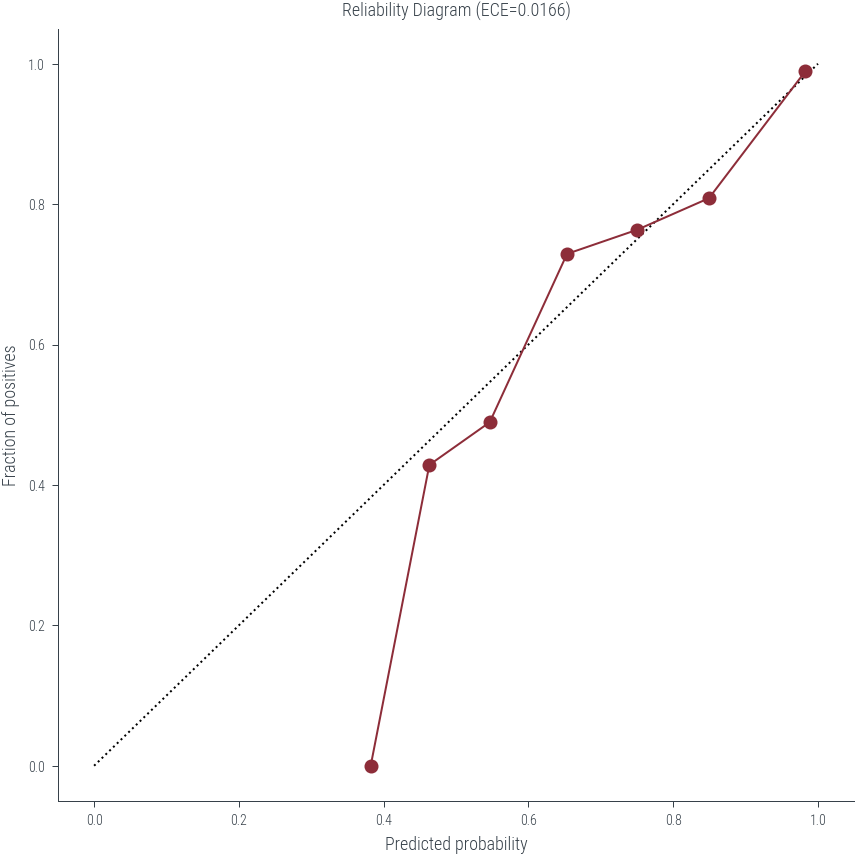

# Histogram of p_hat values

new_df.Most_Probable_Class_Probability.hist(bins=50)
plt.xlim(0, 1)

(0.0, 1.0)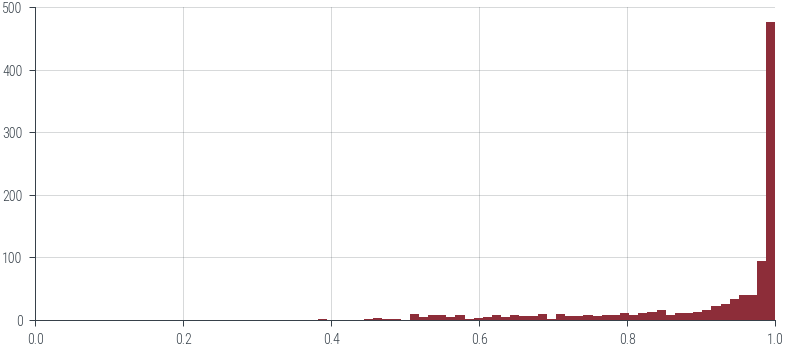

Reliability Diagrams for regression

https://proceedings.mlr.press/v80/kuleshov18a/kuleshov18a.pdf

# Now let us look at the above for regression with heteroscedastic aleatoric uncertainty

X = np.linspace(-3, 3, 1000).reshape(-1, 1)
y = np.sin(X.flatten()) + np.random.normal(0, 0.1, X.shape[0])

plt.scatter(X, y, s=10, alpha=0.5)

<matplotlib.collections.PathCollection at 0x7f351983e700>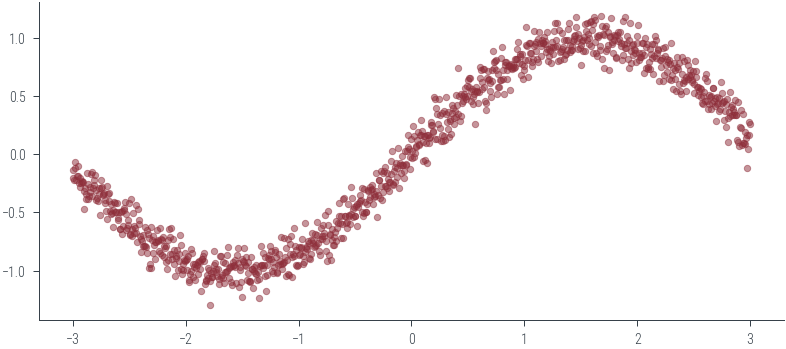

# Use BayesianRidge for regression
from sklearn.linear_model import BayesianRidge

reg = BayesianRidge()
reg.fit(X, y)

BayesianRidge()

# Predict on linspace
X_test = np.linspace(-3, 3, 100).reshape(-1, 1)
y_pred, y_std = reg.predict(X_test, return_std=True)

# Plot the predictions
plt.plot(X_test, y_pred)
plt.fill_between(X_test.flatten(), y_pred - y_std, y_pred + y_std, alpha=0.5)
plt.scatter(X, y, alpha=0.1)

<matplotlib.collections.PathCollection at 0x7f350eb599a0>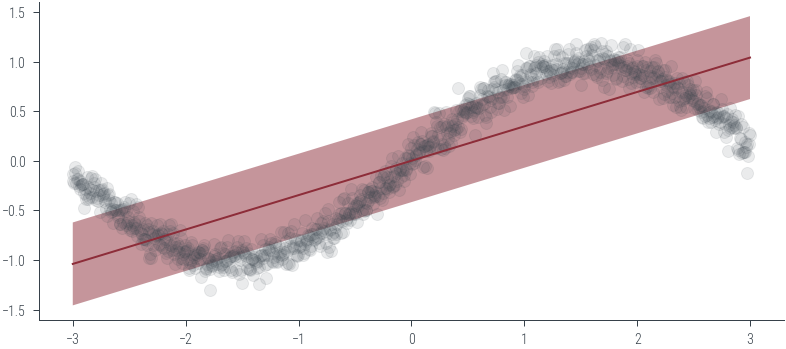

# Within 1\sigma we would like to see 68% of the data points
# Within 2\sigma we would like to see 95% of the data points

# Let us see how many points are within k*sigma of the mean
k = 1
y_pred, y_std = reg.predict(X, return_std=True)
# Check how many points are within k*sigma of the mean
within_k_sigma = np.abs(y - y_pred) < k * y_std
# Fraction of points within k*sigma of the mean
within_k_sigma.mean()

0.585

def within_k_sigma(y, y_pred, y_std, k=1):
    """
    Return the fraction of points within k*sigma of the mean.
    """
    return np.abs(y - y_pred) < k * y_std

# Plot within_k_sigma for k=1, 2, 3, ..

ks = np.arange(1, 6)
within_k_sigma_fractions = [within_k_sigma(y, y_pred, y_std, k=k).mean() for k in ks]

plt.plot(ks, within_k_sigma_fractions, 'o-')
plt.xlabel('k')
plt.ylabel('Fraction of points within k*sigma of the mean')

Text(0, 0.5, 'Fraction of points within k*sigma of the mean')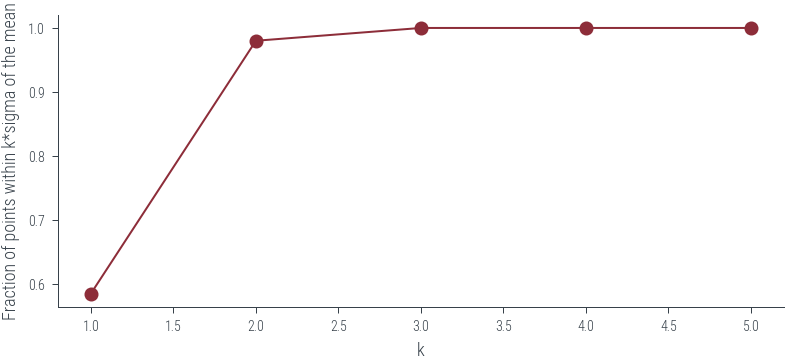

# but, ideally we want 95% of the points to be within 2*sigma of the mean or within 95% CI
# we need a function to map CI to k

from scipy.stats import norm

def ci_to_k(ci):
    """
    Return the value of k corresponding to the given confidence interval.
    """
    return norm.ppf((1 + ci) / 2)

ci_to_k(0.95)

1.959963984540054

ci_to_k(0.68)

0.9944578832097535

# make reliability diagram for regression

percentiles = np.linspace(0, 100, 11)
quantiles = percentiles / 100

ks = ci_to_k(quantiles)

# Get fraction of points within k*sigma of the mean for each k
within_k_sigma_fractions = [within_k_sigma(y, y_pred, y_std, k=k).mean() for k in ks]

plt.plot(quantiles, within_k_sigma_fractions, 'o-')
# Plot ideal
plt.plot([0, 1], [0, 1], 'k:')