Understanding Kernels in Gaussian Processes Regression

Disclaimer

This blog post is forked from GPSS 2019 Lab 1. This is produced only for educational purposes. All credit goes to the GPSS organisers.

# Support for maths
import numpy as np
# Plotting tools
from matplotlib import pyplot as plt
# we use the following for plotting figures in jupyter
%matplotlib inline

import warnings
warnings.filterwarnings('ignore')

# GPy: Gaussian processes library
import GPy
from IPython.display import display

Covariance functions, aka kernels

We will define a covariance function, from hereon referred to as a kernel, using GPy. The most commonly used kernel in machine learning is the Gaussian-form radial basis function (RBF) kernel. It is also commonly referred to as the exponentiated quadratic or squared exponential kernel – all are equivalent.

The definition of the (1-dimensional) RBF kernel has a Gaussian-form, defined as:

\[ \kappa_\mathrm{rbf}(x,x') = \sigma^2\exp\left(-\frac{(x-x')^2}{2\mathscr{l}^2}\right) \]

It has two parameters, described as the variance, \(\sigma^2\) and the lengthscale \(\mathscr{l}\).

In GPy, we define our kernels using the input dimension as the first argument, in the simplest case input_dim=1 for 1-dimensional regression. We can also explicitly define the parameters, but for now we will use the default values:

# Create a 1-D RBF kernel with default parameters
k = GPy.kern.RBF(lengthscale=0.5, input_dim=1, variance=4)
# Preview the kernel's parameters
k

rbf.	value	constraints	priors
variance	4.0	+ve
lengthscale	0.5	+ve

fig, ax = plt.subplots()
from matplotlib.animation import FuncAnimation
from matplotlib import rc
ls = [0.0005, 0.05, 0.25, 0.5, 1., 2., 4.]

X = np.linspace(0.,1.,500)# 500 points evenly spaced over [0,1]
X = X[:,None]
mu = np.zeros((500))

def update(iteration):
    ax.cla()
    k = GPy.kern.RBF(1)
    k.lengthscale = ls[iteration]
    # Calculate the new covariance function at k(x,0)
    C = k.K(X,X)
    Z = np.random.multivariate_normal(mu,C,40)
    for i in range(40):
        ax.plot(X[:],Z[i,:],color='k',alpha=0.2)
    ax.set_title("$\kappa_{rbf}(x,x')$\nLength scale = %s" %k.lengthscale[0]);
    ax.set_ylim((-4, 4))



num_iterations = len(ls)
anim = FuncAnimation(fig, update, frames=np.arange(0, num_iterations-1, 1), interval=500)
plt.close()

rc('animation', html='jshtml')
anim

Once Loop Reflect

In the animation above, as you increase the length scale, the learnt functions keep getting smoother.

fig, ax = plt.subplots()
from matplotlib.animation import FuncAnimation
from matplotlib import rc
var = [0.0005, 0.05, 0.25, 0.5, 1., 2., 4., 9.]

X = np.linspace(0.,1.,500)# 500 points evenly spaced over [0,1]
X = X[:,None]
mu = np.zeros((500))

def update(iteration):
    ax.cla()
    k = GPy.kern.RBF(1)
    k.variance = var[iteration]
    # Calculate the new covariance function at k(x,0)
    C = k.K(X,X)
    Z = np.random.multivariate_normal(mu,C,40)
    for i in range(40):
        ax.plot(X[:],Z[i,:],color='k',alpha=0.2)
    ax.set_title("$\kappa_{rbf}(x,x')$\nVariance = %s" %k.variance[0]);
    ax.set_ylim((-4, 4))



num_iterations = len(ls)
anim = FuncAnimation(fig, update, frames=np.arange(0, num_iterations-1, 1), interval=500)
plt.close()

rc('animation', html='jshtml')
anim

Once Loop Reflect

In the animation above, as you increase the variance, the scale of values increases.

X1 = np.array([1, 2, 3]).reshape(-1, 1)

y1 = np.array([0, 1, 0]).reshape(-1, 1)
y2 = np.array([0, -1, 0]).reshape(-1, 1)
y3 = np.array([0, 10, 0]).reshape(-1, 1)
y4 = np.array([0, 0.3, 0]).reshape(-1, 1)

k = GPy.kern.RBF(lengthscale=0.5, input_dim=1, variance=4)

m = GPy.models.GPRegression(X1, y1, k)
#m.Gaussian_noise = 0.0
m.optimize()
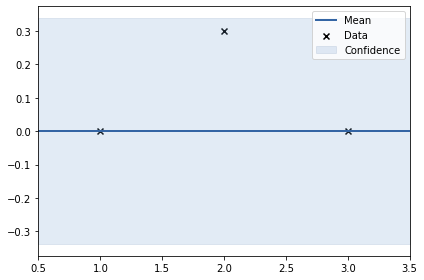
print(k)
m.plot();

  rbf.         |                value  |  constraints  |  priors

  variance     |    0.262031485550043  |      +ve      |        

  lengthscale  |  0.24277532672486218  |      +ve      |        

k = GPy.kern.RBF(lengthscale=0.5, input_dim=1, variance=4)

m = GPy.models.GPRegression(X1, y2, k)
#m.Gaussian_noise = 0.0
m.optimize()
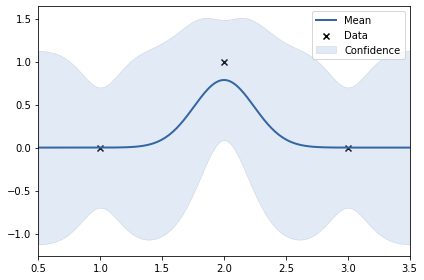
print(k)
m.plot();

  rbf.         |                value  |  constraints  |  priors

  variance     |    0.262031485550043  |      +ve      |        

  lengthscale  |  0.24277532672486218  |      +ve      |        

In the above two examples, the y values are: 0, 1, 0 and 0, -1, 0. This shows smoothness. Thus, length scale can be big (0.24)

k = GPy.kern.RBF(lengthscale=0.5, input_dim=1, variance=4)

m = GPy.models.GPRegression(X1, y3, k)
#m.Gaussian_noise = 0.0
m.optimize()
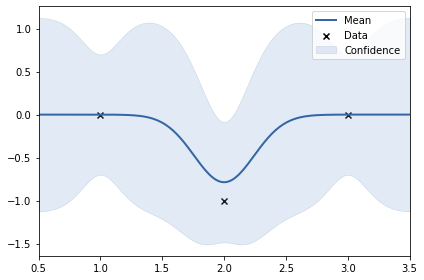
print(k)
m.plot();

  rbf.         |                value  |  constraints  |  priors

  variance     |   16.918792970578004  |      +ve      |        

  lengthscale  |  0.07805339389352635  |      +ve      |        

In the above example, the y values are: 0, 10, 0. The data set is not smooth. Thus, length scale learnt uis very small (0.24). Noise variance of RBF kernel also increased to accomodate the 10.

k = GPy.kern.RBF(lengthscale=0.5, input_dim=1, variance=4)

m = GPy.models.GPRegression(X1, y4, k)
#m.Gaussian_noise = 0.0
m.optimize()
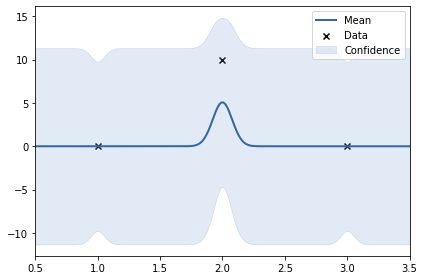
print(k)
m.plot();

  rbf.         |                 value  |  constraints  |  priors

  variance     |  5.90821963086592e-06  |      +ve      |        

  lengthscale  |     2.163452641925496  |      +ve      |        

In the above examples, the y values are: 0, 0.3, 0. The data set is the smoothest amongst the four. Thus, length scale learnt is large (2.1). Noise variance of RBF kernel is also small.