Maximum A-Posteriori (MAP) for parameters of univariate and multivariate normal distribution in PyTorch

ML
PyTorch
Author

Nipun Batra

Published

February 11, 2022

import torch
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt

sns.reset_defaults()
sns.set_context(context="talk", font_scale=1)
%matplotlib inline
%config InlineBackend.figure_format='retina'
dist = torch.distributions

Creating a 1d normal distribution

uv_normal = dist.Normal(loc=0.0, scale=1.0)

Sampling from the distribution

samples = uv_normal.sample(sample_shape=[100])
sns.kdeplot(samples, bw_adjust=2)
sns.despine()

Defining the prior

prior_mu = torch.tensor(5.0, requires_grad=True)
prior = dist.Normal(loc=prior_mu, scale=1.0)
prior
Normal(loc: 5.0, scale: 1.0)

Computing logprob of prior for a mu

def logprob_prior(mu):
    return -prior.log_prob(mu)

Computing logprob of observing data given a mu

stdev_likelihood = 1.0


def log_likelihood(mu, samples):

    to_learn = torch.distributions.Normal(loc=mu, scale=stdev_likelihood)
    return -torch.sum(to_learn.log_prob(samples))
mu = torch.tensor(-2.0, requires_grad=True)

log_likelihood(mu, samples), logprob_prior(mu)
log_likelihood(mu, samples).item()
305.98101806640625
out = {"Logprob_Prior": {}, "LogLikelihood": {}}
for mu_s in torch.linspace(-10, 10, 100):
    t = mu_s.item()
    mu = torch.tensor(mu_s)
    out["Logprob_Prior"][t] = logprob_prior(mu).item()
    out["LogLikelihood"][t] = log_likelihood(mu, samples).item()
/var/folders/1x/wmgn24mn1bbd2vgbqlk98tbc0000gn/T/ipykernel_73152/3102909564.py:4: UserWarning: To copy construct from a tensor, it is recommended to use sourceTensor.clone().detach() or sourceTensor.clone().detach().requires_grad_(True), rather than torch.tensor(sourceTensor).
  mu = torch.tensor(mu_s)
pd.DataFrame(out).plot(subplots=True)
array([<AxesSubplot:>, <AxesSubplot:>], dtype=object)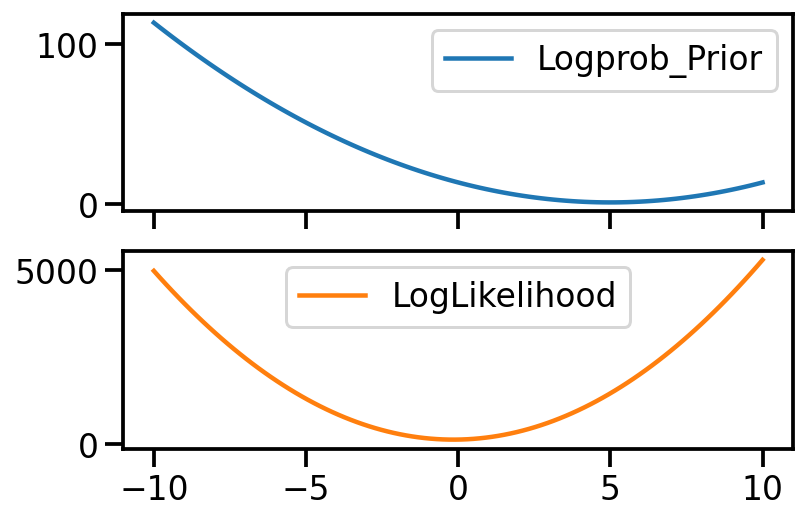

def loss(mu):
    return log_likelihood(mu, samples) + logprob_prior(mu)


mu = torch.tensor(2.0, requires_grad=True)

opt = torch.optim.Adam([mu], lr=0.01)
for i in range(1500):
    loss_val = loss(mu)
    loss_val.backward()
    if i % 100 == 0:
        print(f"Iteration: {i}, Loss: {loss_val.item():0.2f}, Loc: {mu.item():0.6f}")
    opt.step()
    opt.zero_grad()
Iteration: 0, Loss: 374.37, Loc: 2.000000
Iteration: 100, Loss: 222.93, Loc: 1.092788
Iteration: 200, Loss: 166.98, Loc: 0.468122
Iteration: 300, Loss: 152.88, Loc: 0.119012
Iteration: 400, Loss: 150.57, Loc: -0.034995
Iteration: 500, Loss: 150.33, Loc: -0.088207
Iteration: 600, Loss: 150.31, Loc: -0.102667
Iteration: 700, Loss: 150.31, Loc: -0.105761
Iteration: 800, Loss: 150.31, Loc: -0.106279
Iteration: 900, Loss: 150.31, Loc: -0.106346
Iteration: 1000, Loss: 150.31, Loc: -0.106352
Iteration: 1100, Loss: 150.31, Loc: -0.106353
Iteration: 1200, Loss: 150.31, Loc: -0.106353
Iteration: 1300, Loss: 150.31, Loc: -0.106353
Iteration: 1400, Loss: 150.31, Loc: -0.106353

Analytical MAP estimate of location

\(\hat{\theta}_{MAP}=\dfrac{n}{n+\sigma^{2}} \bar{x}+\dfrac{\sigma^{2}}{n+\sigma^{2}} \mu\)

prior_mu
tensor(5., requires_grad=True)
n = samples.shape[0]
sample_mean = samples.mean()
n_plus_variance = n + stdev_likelihood**2

loc_map = ((n * sample_mean) / n_plus_variance) + (
    (stdev_likelihood**2) / (n_plus_variance)
) * prior_mu
loc_map.item()
-0.1063527911901474
torch.allclose(loc_map, mu)
True
Setting 2: Learning location and scale

An important difference from the previous code is that we need to use a transformed variable to ensure scale is positive. We do so by using softplus.

mu = torch.tensor(1.0, requires_grad=True)
scale = torch.tensor(2.0, requires_grad=True)


def log_likelihood(mu, scale, samples):
    scale_softplus = torch.functional.F.softplus(scale)
    to_learn = torch.distributions.Normal(loc=mu, scale=scale_softplus)
    return -torch.sum(to_learn.log_prob(samples))


def loss(mu, scale):
    return log_likelihood(mu, scale, samples) + logprob_prior(mu)


opt = torch.optim.Adam([mu, scale], lr=0.01)
for i in range(1500):
    loss_val = loss(mu, scale)
    loss_val.backward()
    if i % 100 == 0:
        print(
            f"Iteration: {i}, Loss: {loss_val.item():0.2f}, Loc: {mu.item():0.3f}, Scale: {torch.functional.F.softplus(scale).item():0.3f}"
        )
    opt.step()
    opt.zero_grad()
Iteration: 0, Loss: 200.89, Loc: 1.000, Scale: 2.127
Iteration: 100, Loss: 158.51, Loc: 0.086, Scale: 1.282
Iteration: 200, Loss: 149.98, Loc: -0.112, Scale: 0.942
Iteration: 300, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 400, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 500, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 600, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 700, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 800, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 900, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 1000, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 1100, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 1200, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 1300, Loss: 149.98, Loc: -0.112, Scale: 0.943
Iteration: 1400, Loss: 149.98, Loc: -0.112, Scale: 0.943

We can see that our gradient based methods parameters match those of the MLE computed analytically.

mvn = dist.MultivariateNormal(
    loc=torch.tensor([1.0, 1.0]),
    covariance_matrix=torch.tensor([[2.0, 0.5], [0.5, 0.4]]),
)
mle_mvn_loc = mvn_samples = mvn.sample([1000])
loss
loc = torch.tensor([-1.0, 1.0], requires_grad=True)
tril = torch.autograd.Variable(torch.tril(torch.ones(2, 2)), requires_grad=True)
opt = torch.optim.Adam([loc, tril], lr=0.01)

prior = dist.MultivariateNormal(
    loc=torch.tensor([0.0, 0.0]),
    covariance_matrix=torch.tensor([[1.0, 0.0], [0.0, 1.0]])
)


def log_likelihood(loc, tril, samples):
    cov = tril @ tril.t()
    to_learn = torch.distributions.MultivariateNormal(loc=loc, covariance_matrix=cov)
    return -torch.sum(to_learn.log_prob(samples))


def logprob_prior(loc):
    return -prior.log_prob(loc)


def loss(loc, tril, samples):
    return log_likelihood(loc, tril, samples) + logprob_prior(loc)
for i in range(8100):
    to_learn = dist.MultivariateNormal(loc=loc, covariance_matrix=tril @ tril.t())
    loss_value = loss(loc, tril, mvn_samples)
    loss_value.backward()
    if i % 500 == 0:
        print(f"Iteration: {i}, Loss: {loss_value.item():0.2f}, Loc: {loc}")
    opt.step()
    opt.zero_grad()
Iteration: 0, Loss: 7663.86, Loc: tensor([-1.,  1.], requires_grad=True)
Iteration: 500, Loss: 2540.96, Loc: tensor([0.8229, 0.9577], requires_grad=True)
Iteration: 1000, Loss: 2526.40, Loc: tensor([1.0300, 1.0076], requires_grad=True)
Iteration: 1500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 2000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 2500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 3000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 3500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 4000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 4500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 5000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 5500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 6000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 6500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 7000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 7500, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
Iteration: 8000, Loss: 2526.40, Loc: tensor([1.0308, 1.0077], requires_grad=True)
tril@tril.t(),mvn.covariance_matrix, prior.covariance_matrix
(tensor([[1.9699, 0.4505],
         [0.4505, 0.3737]], grad_fn=<MmBackward0>),
 tensor([[2.0000, 0.5000],
         [0.5000, 0.4000]]),
 tensor([[1., 0.],
         [0., 1.]]))
Todo

1. Expand on MVN case
2. Clean up code
3. Visualize, prior, likelihood, MLE, MAP 
4. Shrinkage estimation (reference Murphy book)
5. Inverse Wishart distribution

References

  1. https://stats.stackexchange.com/questions/351549/maximum-likelihood-estimators-multivariate-gaussian
  2. https://forum.pyro.ai/t/mle-for-normal-distribution-parameters/3861/3
  3. https://ericmjl.github.io/notes/stats-ml/estimating-a-multivariate-gaussians-parameters-by-gradient-descent/
  4. https://www.youtube.com/watch?v=KogqeZ_88-g&list=PLD0F06AA0D2E8FFBA&index=32