import jax.numpy as jnp
import jax
from jax import random
import tensorflow_probability.substrates.jax as tfp
tfd = tfp.distributions
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format='retina'random.bernoulli(key=random.PRNGKey(0), p=0.6, shape=(10,)).astype(int).sum()WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)DeviceArray(7, dtype=int32)Probability of getting X heads
from itertools import permutationsset(permutations(['H', 'H', 'H', 'T'], 4 )){('H', 'H', 'H', 'T'),
('H', 'H', 'T', 'H'),
('H', 'T', 'H', 'H'),
('T', 'H', 'H', 'H')}from sympy.utilities.iterables import multiset_permutationslist(multiset_permutations([True, True, False], 3))[[False, True, True], [True, False, True], [True, True, False]]def print_permutations(n_heads=1, n_total=10):
init = ['H']*n_heads
init.extend(['T']*(n_total-n_heads))
permutations = list(multiset_permutations(init, n_total))
return permutations, len(permutations)perm, l = print_permutations()perm[['H', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'T'],
['T', 'H', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'T'],
['T', 'T', 'H', 'T', 'T', 'T', 'T', 'T', 'T', 'T'],
['T', 'T', 'T', 'H', 'T', 'T', 'T', 'T', 'T', 'T'],
['T', 'T', 'T', 'T', 'H', 'T', 'T', 'T', 'T', 'T'],
['T', 'T', 'T', 'T', 'T', 'H', 'T', 'T', 'T', 'T'],
['T', 'T', 'T', 'T', 'T', 'T', 'H', 'T', 'T', 'T'],
['T', 'T', 'T', 'T', 'T', 'T', 'T', 'H', 'T', 'T'],
['T', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'H', 'T'],
['T', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'T', 'H']]l10num_sequences = {}
for n_heads in range(0, 11, 1):
_, num_sequences[n_heads] = print_permutations(n_heads=n_heads, n_total=10)num_sequences = pd.Series(num_sequences)
num_sequences0 1
1 10
2 45
3 120
4 210
5 252
6 210
7 120
8 45
9 10
10 1
dtype: int64num_sequences.plot(xlabel="Heads", ylabel="Permutations")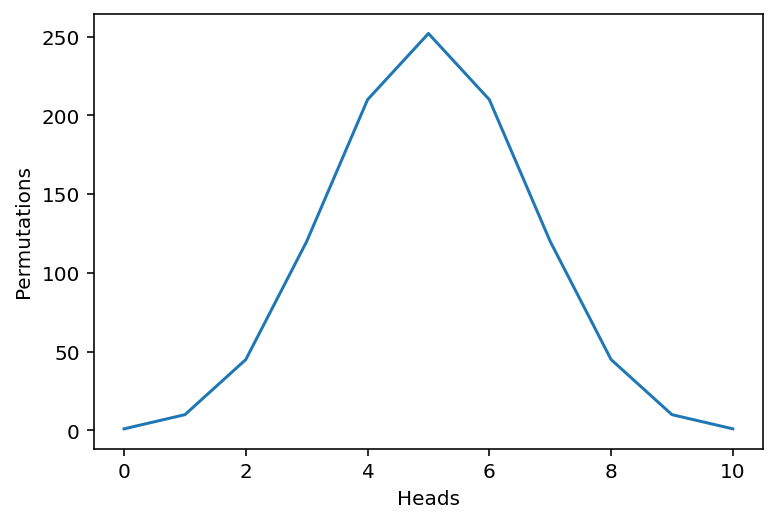
from math import comb
comb(10, 3)120pd.Series(list(map(partial(comb, 10), range(0, 11))))0 1
1 10
2 45
3 120
4 210
5 252
6 210
7 120
8 45
9 10
10 1
dtype: int64### Probability of given sequencedef prob_sequence(n_heads = 5, n_total = 10, p_head = 0.3):
return (p_head**n_heads)*(1-p_head)**(n_total-n_heads)from functools import partialprob_sequence(0, 10, 0.3)0.02824752489999998prob_sequence_fixed_p = partial(prob_sequence, n_total=10, p_head=0.3)probs = prob_sequence_fixed_p(num_sequences.index)*num_sequences
probs0 0.028248
1 0.121061
2 0.233474
3 0.266828
4 0.200121
5 0.102919
6 0.036757
7 0.009002
8 0.001447
9 0.000138
10 0.000006
dtype: float64probs.plot()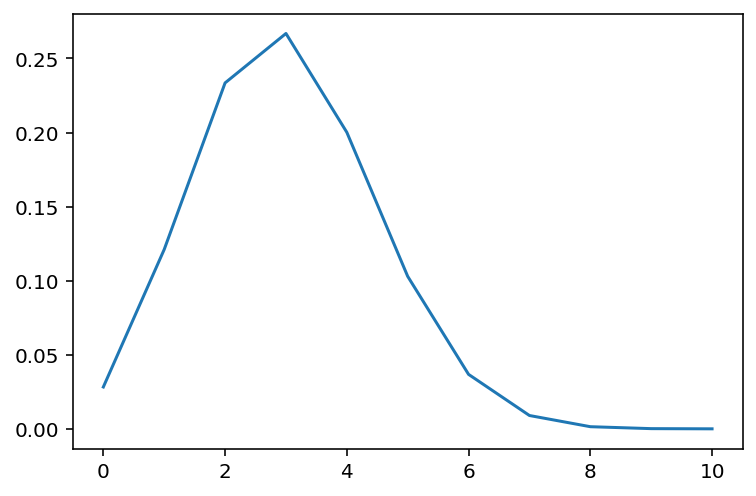
import richrich.inspect(tfd.Binomial)╭───── <class 'tensorflow_probability.substrates.jax.distributions.binomial.Binomial'> ─────╮ │ class Binomial(total_count, logits=None, probs=None, validate_args=False, │ │ allow_nan_stats=True, name=None): │ │ │ │ Binomial distribution. │ │ │ │ allow_nan_stats = <property object at 0x1a7594310> │ │ batch_shape = <property object at 0x1a7594400> │ │ dtype = <property object at 0x1a7594220> │ │ event_shape = <property object at 0x1a7594450> │ │ experimental_shard_axis_names = <property object at 0x1a75943b0> │ │ logits = <property object at 0x1a75f79a0> │ │ name = <property object at 0x1a75941d0> │ │ parameters = <property object at 0x1a7594270> │ │ probs = <property object at 0x1a75f79f0> │ │ reparameterization_type = <property object at 0x1a75942c0> │ │ total_count = <property object at 0x1a75f7950> │ │ trainable_variables = <property object at 0x115bf0f40> │ │ validate_args = <property object at 0x1a7594360> │ │ variables = <property object at 0x115bf0f90> │ ╰───────────────────────────────────────────────────────────────────────────────────────────╯
from scipy.special import comb as scombfrom dataclasses import dataclass
@dataclass
class OurBinomial:
total_count: int = 10
probs: float = 0.5
def __repr__(self):
return (
"Binomial distribution"
+ "\n"
+ "---------------------\n"
+ f"P(H) = {self.probs}\nTotal Count = {self.total_count}"
)
def mode(self):
return self.probs * self.total_count
def prob(self, observed_num_heads):
# (N choose K)*(p**n_h)*(1-p)**n_t
return (
comb(self.total_count, observed_num_heads)
* (self.probs**observed_num_heads)
* (1 - self.probs) ** (self.total_count - observed_num_heads)
)
def logprob(self, observed_num_heads):
return (
jnp.log(comb(self.total_count, observed_num_heads))
+ observed_num_heads * jnp.log(self.probs)
+ (self.total_count - observed_num_heads) * jnp.log(1 - self.probs)
)c = OurBinomial(probs=0.3)
cBinomial distribution
---------------------
P(H) = 0.3
Total Count = 10c.total_count10tfp_bin = tfd.Binomial(total_count=10, probs=0.3)tfp_bin.mode()DeviceArray(3., dtype=float32)c.mode()3.0tfp_bin.prob(2)DeviceArray(0.23347428, dtype=float32)comb(10, 3)120c.prob(2)0.23347444049999988jnp.allclose(c.prob(2), tfp_bin.prob(2))DeviceArray(True, dtype=bool)tfp_bin.log_prob(2)DeviceArray(-1.4546833, dtype=float32)c.logprob(2)DeviceArray(-1.4546828, dtype=float32)binomial_dict = {}
# Divide hour in 10 intervals
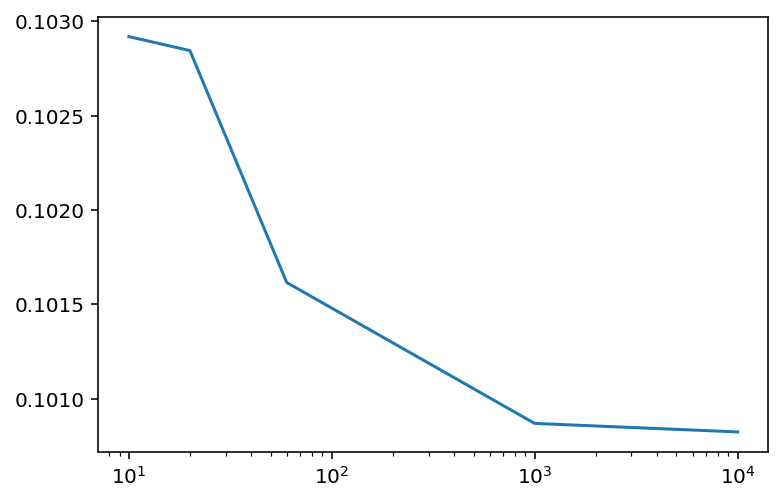
binomial_dict[10] = OurBinomial(total_count=10, probs=0.3).prob(5)binomial_dict{10: 0.10291934519999994}for interval in [10, 20, 60, 1000, 10000]:
binomial_dict[interval] = OurBinomial(total_count=interval, probs=3.0/interval).prob(5)binomial_dict{10: 0.10291934519999994,
20: 0.10284517954557212,
60: 0.10161579161609695,
1000: 0.10086908328293617,
10000: 0.10082385299843205}pd.Series(binomial_dict).plot(logx=True)