CDF for Discrete Random Variables

Understanding cumulative distribution functions for discrete random variables with categorical distributions and practical examples of logistic regression

Keywords

CDF, cumulative distribution function, discrete random variables, categorical distribution, logistic regression, PyTorch

import matplotlib.pyplot as plt
import numpy as np
import torch 
import torch.nn as nn

import pandas as pd
# Retina mode
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

# Set random seed
torch.manual_seed(42)

<torch._C.Generator at 0x135180ab0>

probs = [0.1, 0.4, 0.2, 0.3]
dist = torch.distributions.Categorical(probs=torch.tensor(probs))

dist

Categorical(probs: torch.Size([4]))

pd.Series(dist.sample(torch.Size([1000]))).value_counts().sort_index()

0     90
1    409
2    187
3    314
Name: count, dtype: int64

# Generate 2D input features
n_samples = 1000
X1 = torch.distributions.Uniform(0, 5).sample((n_samples, 1))  # Feature 1
X2 = torch.distributions.Uniform(0, 5).sample((n_samples, 1))  # Feature 2

# True weights and bias
w1, w2, b = 1.2, -0.8, -2.5  

# Compute logits and apply sigmoid
logits = w1 * X1 + w2 * X2 + b
prob_Y = torch.sigmoid(logits)  # Probabilities

prob_Y

tensor([[0.4690],
        [0.8697],
        [0.2377],
        [0.6852],
        [0.2472],
        [0.5074],
        [0.0922],
        [0.7336],
        [0.8787],
        [0.0406],
        [0.6429],
        [0.6637],
        [0.8729],
        [0.2455],
        [0.4179],
        [0.0462],
        [0.9018],
        [0.1551],
        [0.0173],
        [0.1364],
        [0.2652],
        [0.2519],
        [0.2691],
        [0.8527],
        [0.0068],
        [0.0701],
        [0.0393],
        [0.1062],
        [0.1793],
        [0.0372],
        [0.5522],
        [0.0402],
        [0.7888],
        [0.6758],
        [0.0772],
        [0.1758],
        [0.1189],
        [0.8798],
        [0.2317],
        [0.0974],
        [0.7143],
        [0.0202],
        [0.4330],
        [0.6808],
        [0.7392],
        [0.1329],
        [0.4755],
        [0.1541],
        [0.3953],
        [0.0859],
        [0.0016],
        [0.0859],
        [0.0707],
        [0.8696],
        [0.0688],
        [0.4360],
        [0.4305],
        [0.3274],
        [0.7977],
        [0.1249],
        [0.5691],
        [0.0089],
        [0.0923],
        [0.0116],
        [0.7033],
        [0.0389],
        [0.9026],
        [0.0113],
        [0.0087],
        [0.0079],
        [0.4398],
        [0.1479],
        [0.7938],
        [0.0074],
        [0.0228],
        [0.0089],
        [0.0534],
        [0.4375],
        [0.7883],
        [0.8199],
        [0.1195],
        [0.0536],
        [0.7972],
        [0.2862],
        [0.5475],
        [0.0290],
        [0.1672],
        [0.0067],
        [0.1216],
        [0.8010],
        [0.1646],
        [0.0328],
        [0.8813],
        [0.4557],
        [0.0046],
        [0.0383],
        [0.9207],
        [0.0155],
        [0.0318],
        [0.0032],
        [0.1341],
        [0.1285],
        [0.3706],
        [0.0035],
        [0.3584],
        [0.0085],
        [0.0116],
        [0.0246],
        [0.0215],
        [0.0143],
        [0.9115],
        [0.7215],
        [0.5481],
        [0.0028],
        [0.0500],
        [0.0420],
        [0.4277],
        [0.0035],
        [0.0182],
        [0.0180],
        [0.3848],
        [0.2725],
        [0.1439],
        [0.0863],
        [0.0055],
        [0.2094],
        [0.0317],
        [0.0028],
        [0.5034],
        [0.0586],
        [0.9528],
        [0.0766],
        [0.0242],
        [0.9202],
        [0.0134],
        [0.1375],
        [0.0209],
        [0.0018],
        [0.6780],
        [0.3229],
        [0.3414],
        [0.0243],
        [0.5663],
        [0.1166],
        [0.1113],
        [0.5040],
        [0.7373],
        [0.9401],
        [0.5430],
        [0.0139],
        [0.7203],
        [0.0124],
        [0.0808],
        [0.0160],
        [0.9173],
        [0.0179],
        [0.1390],
        [0.1397],
        [0.7374],
        [0.0071],
        [0.7449],
        [0.1415],
        [0.0649],
        [0.0029],
        [0.7889],
        [0.0241],
        [0.1800],
        [0.7164],
        [0.6379],
        [0.0617],
        [0.0508],
        [0.1972],
        [0.6204],
        [0.0813],
        [0.0056],
        [0.0244],
        [0.0077],
        [0.2261],
        [0.3260],
        [0.0143],
        [0.2764],
        [0.4105],
        [0.6875],
        [0.2774],
        [0.4553],
        [0.7025],
        [0.4154],
        [0.1725],
        [0.0688],
        [0.0773],
        [0.2032],
        [0.0181],
        [0.2384],
        [0.9317],
        [0.4372],
        [0.3650],
        [0.4109],
        [0.2889],
        [0.3479],
        [0.4569],
        [0.0386],
        [0.1222],
        [0.8519],
        [0.0917],
        [0.2874],
        [0.1328],
        [0.0153],
        [0.0168],
        [0.0178],
        [0.1498],
        [0.1939],
        [0.7941],
        [0.0043],
        [0.0068],
        [0.2717],
        [0.3926],
        [0.0714],
        [0.0912],
        [0.2274],
        [0.1253],
        [0.1548],
        [0.5459],
        [0.0305],
        [0.3112],
        [0.0043],
        [0.9017],
        [0.2792],
        [0.0876],
        [0.0157],
        [0.0389],
        [0.0073],
        [0.5978],
        [0.3535],
        [0.5908],
        [0.1898],
        [0.5297],
        [0.2536],
        [0.0130],
        [0.0135],
        [0.0027],
        [0.6854],
        [0.0522],
        [0.0775],
        [0.0632],
        [0.0320],
        [0.0212],
        [0.1663],
        [0.4284],
        [0.1848],
        [0.5393],
        [0.0971],
        [0.1523],
        [0.1591],
        [0.0594],
        [0.1385],
        [0.0020],
        [0.6491],
        [0.0076],
        [0.3805],
        [0.8249],
        [0.5432],
        [0.0042],
        [0.8772],
        [0.1644],
        [0.0875],
        [0.4281],
        [0.3085],
        [0.0614],
        [0.1262],
        [0.1158],
        [0.4476],
        [0.0059],
        [0.7236],
        [0.5122],
        [0.9547],
        [0.0268],
        [0.0034],
        [0.1269],
        [0.4547],
        [0.0058],
        [0.3243],
        [0.0574],
        [0.1720],
        [0.1343],
        [0.2229],
        [0.0219],
        [0.0033],
        [0.9415],
        [0.5935],
        [0.0582],
        [0.0232],
        [0.0202],
        [0.0024],
        [0.0227],
        [0.1436],
        [0.0084],
        [0.1765],
        [0.4679],
        [0.0520],
        [0.0276],
        [0.3989],
        [0.0865],
        [0.0738],
        [0.0310],
        [0.0538],
        [0.4719],
        [0.0175],
        [0.6643],
        [0.0717],
        [0.2207],
        [0.6581],
        [0.1212],
        [0.0091],
        [0.5362],
        [0.3897],
        [0.5126],
        [0.7488],
        [0.7894],
        [0.3925],
        [0.2507],
        [0.0973],
        [0.0892],
        [0.6295],
        [0.4406],
        [0.1529],
        [0.1186],
        [0.0113],
        [0.0021],
        [0.1150],
        [0.0482],
        [0.8805],
        [0.2454],
        [0.0035],
        [0.0044],
        [0.8107],
        [0.0069],
        [0.0515],
        [0.4856],
        [0.0080],
        [0.2625],
        [0.2149],
        [0.2317],
        [0.0353],
        [0.0090],
        [0.0166],
        [0.1212],
        [0.9087],
        [0.0258],
        [0.1467],
        [0.3867],
        [0.3478],
        [0.7219],
        [0.5131],
        [0.5104],
        [0.0028],
        [0.2580],
        [0.8291],
        [0.0395],
        [0.0280],
        [0.8736],
        [0.2135],
        [0.0247],
        [0.0914],
        [0.1309],
        [0.2388],
        [0.7147],
        [0.5993],
        [0.0881],
        [0.0025],
        [0.0412],
        [0.7522],
        [0.1615],
        [0.0706],
        [0.5131],
        [0.0120],
        [0.0252],
        [0.0513],
        [0.5335],
        [0.3664],
        [0.0042],
        [0.2806],
        [0.1637],
        [0.1168],
        [0.9396],
        [0.0373],
        [0.7879],
        [0.0925],
        [0.0391],
        [0.6586],
        [0.4116],
        [0.1996],
        [0.0494],
        [0.2710],
        [0.6425],
        [0.1510],
        [0.0312],
        [0.0179],
        [0.1739],
        [0.6685],
        [0.2275],
        [0.1530],
        [0.9160],
        [0.4186],
        [0.1890],
        [0.2847],
        [0.0327],
        [0.0187],
        [0.0628],
        [0.1278],
        [0.3404],
        [0.1098],
        [0.0375],
        [0.7807],
        [0.6327],
        [0.7904],
        [0.0507],
        [0.1858],
        [0.3649],
        [0.0336],
        [0.0142],
        [0.1073],
        [0.0164],
        [0.0245],
        [0.8529],
        [0.5046],
        [0.5838],
        [0.1484],
        [0.0258],
        [0.1378],
        [0.5009],
        [0.1275],
        [0.0463],
        [0.0377],
        [0.1537],
        [0.1114],
        [0.5183],
        [0.0190],
        [0.0583],
        [0.3773],
        [0.1361],
        [0.2197],
        [0.6813],
        [0.2385],
        [0.9250],
        [0.9642],
        [0.1617],
        [0.0100],
        [0.4980],
        [0.9302],
        [0.0457],
        [0.1462],
        [0.0613],
        [0.0062],
        [0.0611],
        [0.2581],
        [0.6507],
        [0.0583],
        [0.6322],
        [0.0657],
        [0.0992],
        [0.5305],
        [0.1600],
        [0.3603],
        [0.0488],
        [0.6136],
        [0.1191],
        [0.0036],
        [0.0577],
        [0.4877],
        [0.3272],
        [0.7177],
        [0.4588],
        [0.7115],
        [0.0364],
        [0.2061],
        [0.3108],
        [0.0613],
        [0.0117],
        [0.0795],
        [0.4676],
        [0.5647],
        [0.0231],
        [0.1328],
        [0.5421],
        [0.0562],
        [0.0614],
        [0.3270],
        [0.0339],
        [0.8109],
        [0.3840],
        [0.5580],
        [0.6581],
        [0.5215],
        [0.4812],
        [0.4216],
        [0.5801],
        [0.8010],
        [0.6829],
        [0.0294],
        [0.0095],
        [0.0193],
        [0.0555],
        [0.2013],
        [0.8739],
        [0.5182],
        [0.8575],
        [0.0095],
        [0.0300],
        [0.0588],
        [0.0581],
        [0.4170],
        [0.0025],
        [0.1793],
        [0.0060],
        [0.0250],
        [0.0052],
        [0.4422],
        [0.0052],
        [0.3186],
        [0.2248],
        [0.0405],
        [0.4789],
        [0.0483],
        [0.1727],
        [0.5538],
        [0.0335],
        [0.4634],
        [0.1829],
        [0.2329],
        [0.3739],
        [0.0957],
        [0.0156],
        [0.3449],
        [0.8196],
        [0.6699],
        [0.4111],
        [0.0098],
        [0.3198],
        [0.0751],
        [0.8296],
        [0.0686],
        [0.0258],
        [0.0505],
        [0.0505],
        [0.6845],
        [0.1587],
        [0.3579],
        [0.6190],
        [0.9235],
        [0.2053],
        [0.1562],
        [0.4789],
        [0.0443],
        [0.2962],
        [0.0232],
        [0.0190],
        [0.5996],
        [0.6140],
        [0.7862],
        [0.9355],
        [0.4863],
        [0.5655],
        [0.0436],
        [0.0308],
        [0.0309],
        [0.0590],
        [0.0157],
        [0.0254],
        [0.0145],
        [0.0126],
        [0.0280],
        [0.0055],
        [0.0610],
        [0.6977],
        [0.6296],
        [0.1038],
        [0.1875],
        [0.3234],
        [0.0475],
        [0.0674],
        [0.7886],
        [0.0208],
        [0.6382],
        [0.6671],
        [0.2659],
        [0.1304],
        [0.0330],
        [0.1543],
        [0.1324],
        [0.0923],
        [0.6481],
        [0.4782],
        [0.0137],
        [0.4810],
        [0.0242],
        [0.0645],
        [0.2477],
        [0.0396],
        [0.8759],
        [0.0614],
        [0.2093],
        [0.2825],
        [0.0732],
        [0.0819],
        [0.0994],
        [0.0042],
        [0.0639],
        [0.0714],
        [0.6146],
        [0.5548],
        [0.5720],
        [0.0173],
        [0.0950],
        [0.9247],
        [0.0979],
        [0.5093],
        [0.3201],
        [0.0249],
        [0.0115],
        [0.8606],
        [0.3280],
        [0.2417],
        [0.0065],
        [0.0185],
        [0.0386],
        [0.0495],
        [0.0566],
        [0.8324],
        [0.0054],
        [0.1783],
        [0.0084],
        [0.1398],
        [0.5463],
        [0.5990],
        [0.2893],
        [0.2422],
        [0.0921],
        [0.0408],
        [0.0046],
        [0.0630],
        [0.2670],
        [0.0066],
        [0.9150],
        [0.5427],
        [0.0191],
        [0.1254],
        [0.0957],
        [0.3615],
        [0.1072],
        [0.2503],
        [0.7266],
        [0.0921],
        [0.5816],
        [0.4543],
        [0.1018],
        [0.9215],
        [0.0393],
        [0.1537],
        [0.0449],
        [0.8551],
        [0.0236],
        [0.3884],
        [0.0032],
        [0.3583],
        [0.7975],
        [0.1741],
        [0.7627],
        [0.0478],
        [0.4580],
        [0.0336],
        [0.2849],
        [0.2970],
        [0.9362],
        [0.2849],
        [0.0084],
        [0.3964],
        [0.0635],
        [0.4038],
        [0.0035],
        [0.2056],
        [0.7709],
        [0.2959],
        [0.0089],
        [0.1077],
        [0.0589],
        [0.5707],
        [0.0962],
        [0.0793],
        [0.0674],
        [0.0335],
        [0.7049],
        [0.8910],
        [0.0836],
        [0.3845],
        [0.5714],
        [0.7929],
        [0.6587],
        [0.5552],
        [0.0545],
        [0.8679],
        [0.8363],
        [0.0228],
        [0.0075],
        [0.0453],
        [0.1558],
        [0.0073],
        [0.1370],
        [0.4195],
        [0.0152],
        [0.1042],
        [0.0471],
        [0.1086],
        [0.6888],
        [0.0051],
        [0.4637],
        [0.9148],
        [0.3310],
        [0.0220],
        [0.0207],
        [0.1868],
        [0.0823],
        [0.2680],
        [0.8058],
        [0.9286],
        [0.1681],
        [0.1451],
        [0.1451],
        [0.0671],
        [0.0082],
        [0.1195],
        [0.8149],
        [0.0024],
        [0.0062],
        [0.6743],
        [0.4562],
        [0.6410],
        [0.0143],
        [0.0469],
        [0.7715],
        [0.4464],
        [0.5066],
        [0.1339],
        [0.5612],
        [0.5935],
        [0.0075],
        [0.0167],
        [0.5136],
        [0.0040],
        [0.0411],
        [0.5657],
        [0.0792],
        [0.0777],
        [0.1271],
        [0.0341],
        [0.6242],
        [0.0441],
        [0.0383],
        [0.7237],
        [0.0076],
        [0.3616],
        [0.1653],
        [0.2611],
        [0.4183],
        [0.0433],
        [0.0674],
        [0.7030],
        [0.2125],
        [0.0033],
        [0.0105],
        [0.5878],
        [0.2345],
        [0.7199],
        [0.1536],
        [0.0522],
        [0.0208],
        [0.1033],
        [0.0328],
        [0.5261],
        [0.4477],
        [0.4163],
        [0.0638],
        [0.0860],
        [0.7403],
        [0.3582],
        [0.0382],
        [0.0144],
        [0.3440],
        [0.1347],
        [0.2414],
        [0.9490],
        [0.0595],
        [0.9154],
        [0.8628],
        [0.0031],
        [0.6427],
        [0.0366],
        [0.0776],
        [0.3921],
        [0.0062],
        [0.8658],
        [0.2734],
        [0.7700],
        [0.0047],
        [0.6233],
        [0.0978],
        [0.0369],
        [0.4760],
        [0.4007],
        [0.3911],
        [0.1022],
        [0.0443],
        [0.6452],
        [0.5626],
        [0.1089],
        [0.5314],
        [0.0162],
        [0.6265],
        [0.8584],
        [0.2519],
        [0.2426],
        [0.8181],
        [0.5241],
        [0.0241],
        [0.0273],
        [0.0294],
        [0.3048],
        [0.2815],
        [0.1653],
        [0.6694],
        [0.0173],
        [0.4302],
        [0.2016],
        [0.0251],
        [0.1268],
        [0.0075],
        [0.5129],
        [0.0309],
        [0.0977],
        [0.0888],
        [0.1067],
        [0.5135],
        [0.0031],
        [0.0084],
        [0.0379],
        [0.3944],
        [0.0491],
        [0.1070],
        [0.0736],
        [0.1812],
        [0.9447],
        [0.1928],
        [0.1918],
        [0.0043],
        [0.1300],
        [0.0261],
        [0.1692],
        [0.8610],
        [0.8094],
        [0.9622],
        [0.5234],
        [0.1729],
        [0.0978],
        [0.5527],
        [0.0086],
        [0.2799],
        [0.3916],
        [0.6266],
        [0.3144],
        [0.0426],
        [0.0029],
        [0.0657],
        [0.4495],
        [0.1725],
        [0.1724],
        [0.4098],
        [0.0512],
        [0.8470],
        [0.1267],
        [0.5247],
        [0.1115],
        [0.7646],
        [0.7213],
        [0.0759],
        [0.3569],
        [0.3375],
        [0.8672],
        [0.7596],
        [0.1475],
        [0.0044],
        [0.4780],
        [0.0581],
        [0.0251],
        [0.4568],
        [0.2024],
        [0.7446],
        [0.6320],
        [0.0314],
        [0.0765],
        [0.0181],
        [0.1966],
        [0.5667],
        [0.8577],
        [0.9013],
        [0.1643],
        [0.0776],
        [0.1805],
        [0.0631],
        [0.1894],
        [0.3725],
        [0.0367],
        [0.1032],
        [0.8510],
        [0.3935],
        [0.8488],
        [0.9634],
        [0.0439],
        [0.0918],
        [0.5004],
        [0.0232],
        [0.2922],
        [0.0592],
        [0.6902],
        [0.0502],
        [0.2931],
        [0.5467],
        [0.0902],
        [0.0438],
        [0.7579],
        [0.0144],
        [0.0310],
        [0.9566],
        [0.0983],
        [0.1246],
        [0.0175],
        [0.3579],
        [0.1215],
        [0.0063],
        [0.8350],
        [0.0783],
        [0.0673],
        [0.0044],
        [0.1932],
        [0.0166],
        [0.0619],
        [0.0126],
        [0.0981],
        [0.1415],
        [0.0975],
        [0.0028],
        [0.7217],
        [0.1342],
        [0.0666],
        [0.8163],
        [0.5906],
        [0.8264],
        [0.0062],
        [0.1267],
        [0.0576],
        [0.4529],
        [0.1712],
        [0.0178],
        [0.1451],
        [0.0375],
        [0.1448],
        [0.1852],
        [0.9204],
        [0.6197],
        [0.0180],
        [0.3411],
        [0.0445],
        [0.1539],
        [0.4608],
        [0.5943],
        [0.2118],
        [0.8577],
        [0.0662],
        [0.2722],
        [0.6509],
        [0.5460],
        [0.4635],
        [0.2292],
        [0.0513],
        [0.2066],
        [0.5374],
        [0.0059],
        [0.2224],
        [0.1254],
        [0.3754],
        [0.5258],
        [0.0939],
        [0.1778],
        [0.2772],
        [0.0344],
        [0.0388],
        [0.9426],
        [0.1209],
        [0.2947],
        [0.0870],
        [0.4037],
        [0.0158]])

# Sample class labels
Y = torch.distributions.Bernoulli(prob_Y).sample()

# Convert to NumPy for visualization
X1_np, X2_np, Y_np = X1.numpy(), X2.numpy(), Y.numpy()

# Plot data points
plt.scatter(X1_np[Y_np == 0], X2_np[Y_np == 0], color="blue", label="Class 0", alpha=0.5)
plt.scatter(X1_np[Y_np == 1], X2_np[Y_np == 1], color="red", label="Class 1", alpha=0.5)
plt.xlabel("Feature 1 (X1)")
plt.ylabel("Feature 2 (X2)")
plt.legend()
plt.title("Generated 2D Logistic Regression Data")

Text(0.5, 1.0, 'Generated 2D Logistic Regression Data')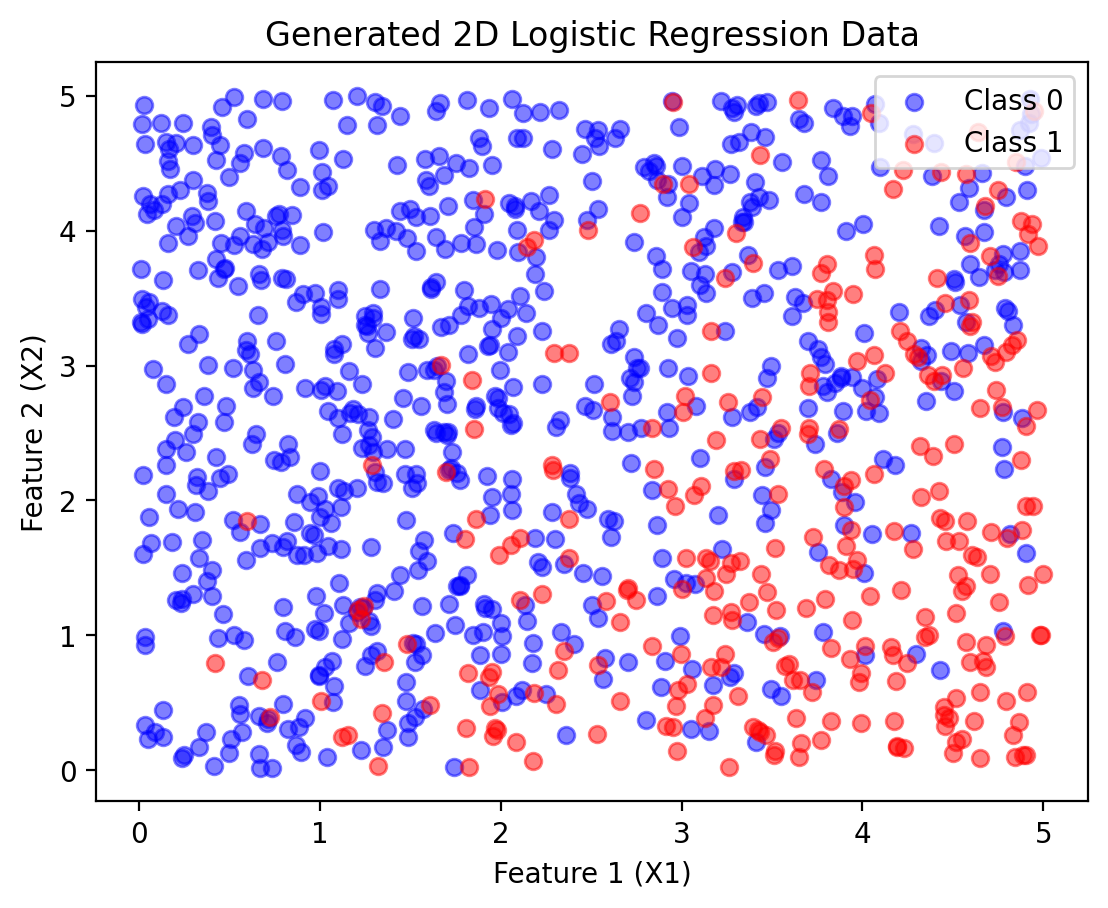

import torch.nn as nn
import torch.optim as optim

# Stack X1 and X2 into a single tensor
X_train = torch.cat((X1, X2), dim=1)

# Define logistic regression model
class LogisticRegression2D(nn.Module):
    def __init__(self):
        super(LogisticRegression2D, self).__init__()
        self.linear = nn.Linear(2, 1)  # Two inputs, one output

    def forward(self, x):
        return torch.sigmoid(self.linear(x))  # Sigmoid activation

# Initialize model
model = LogisticRegression2D()
loss_fn = nn.BCELoss()  # Binary cross-entropy loss
optimizer = optim.SGD(model.parameters(), lr=0.01)

# Training loop
epochs = 1000
for epoch in range(epochs):
    optimizer.zero_grad()
    Y_pred = model(X_train)  # Forward pass
    loss = loss_fn(Y_pred, Y.view(-1, 1))  # Compute loss
    loss.backward()  # Backpropagation
    optimizer.step()  # Update weights

    if epoch % 200 == 0:
        print(f"Epoch {epoch}, Loss: {loss.item():.4f}")

# Extract learned parameters
w1_learned, w2_learned = model.linear.weight[0].detach().numpy()
b_learned = model.linear.bias[0].detach().numpy()
print(f"Learned Parameters: w1 = {w1_learned:.4f}, w2 = {w2_learned:.4f}, b = {b_learned:.4f}")

Epoch 0, Loss: 2.0864
Epoch 200, Loss: 0.4884
Epoch 400, Loss: 0.4536
Epoch 600, Loss: 0.4395
Epoch 800, Loss: 0.4318
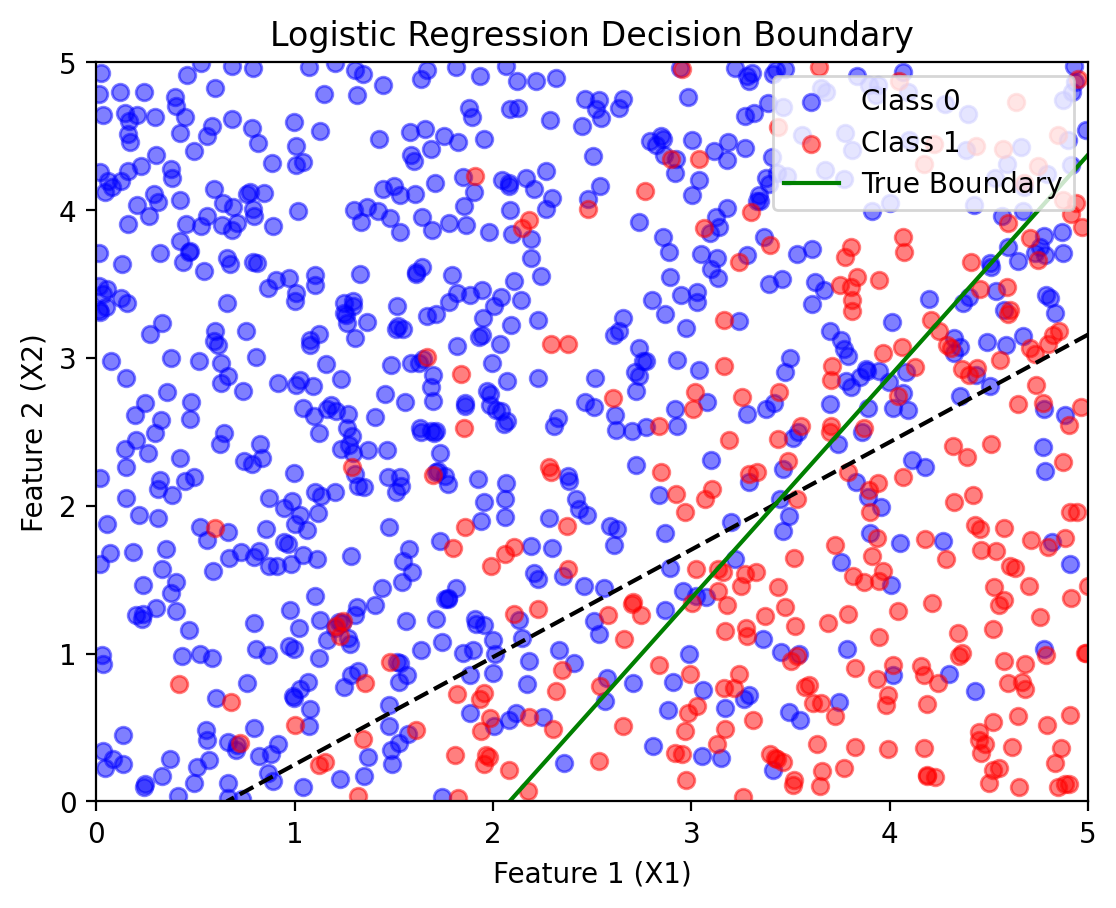
Learned Parameters: w1 = 0.6339, w2 = -0.8716, b = -0.4170

def plot_decision_boundary(model, X1_np, X2_np, Y_np, w1_true, w2_true, b_true):
    """Plots the true and learned decision boundaries."""
    
    # Generate mesh grid
    x1_vals = np.linspace(0, 5, 100)
    x2_vals = np.linspace(0, 5, 100)
    X1_grid, X2_grid = np.meshgrid(x1_vals, x2_vals)

    # Compute model's learned decision boundary
    with torch.no_grad():
        Z = model(torch.tensor(np.c_[X1_grid.ravel(), X2_grid.ravel()], dtype=torch.float32))
        Z = Z.view(X1_grid.shape).numpy()

    # Compute true decision boundary
    x1_boundary = np.linspace(0,5, 100)
    x2_boundary_true = - (w1_true / w2_true) * x1_boundary - (b_true / w2_true)

    # Plot data points
    plt.scatter(X1_np[Y_np == 0], X2_np[Y_np == 0], color="blue", label="Class 0", alpha=0.5)
    plt.scatter(X1_np[Y_np == 1], X2_np[Y_np == 1], color="red", label="Class 1", alpha=0.5)

    # Plot learned decision boundary
    plt.contour(X1_grid, X2_grid, Z, levels=[0.5], colors="black", linestyles="dashed", label="Learned Boundary")

    # Plot true decision boundary
    plt.plot(x1_boundary, x2_boundary_true, color="green", linestyle="solid", label="True Boundary")

    plt.xlabel("Feature 1 (X1)")
    plt.ylabel("Feature 2 (X2)")
    plt.legend()
    plt.title("Logistic Regression Decision Boundary")
    plt.ylim([0, 5])


# Call the function with true and learned parameters
plot_decision_boundary(model, X1_np, X2_np, Y_np, w1_true=1.2, w2_true=-0.8, b_true=-2.5)