Sum of Random Variables

Understanding the distribution of sums of random variables through simulation and theory, covering both discrete and continuous cases

Keywords

random variables, sum, normal distribution, categorical distribution, convolution, central limit theorem

import torch
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%config InlineBackend.figure_format = 'retina'

Sum of Random Variables

This notebook explores what happens when we add random variables together. We’ll examine both continuous and discrete cases, comparing simulation results with theoretical predictions.

Learning Objectives

• Understand how sums of random variables behave
• Compare empirical distributions with theoretical results
• Explore the convolution property for independent random variables
• Visualize distributions using kernel density estimation

Let’s start by importing the necessary libraries:

Case 1: Sum of Normal Random Variables

When we add independent normal random variables, the result is also normally distributed. Let’s verify this through simulation.

We have: - X ~ N(0, 1) (standard normal) - Y ~ N(0, 2) (normal with standard deviation 2)

Theory tells us that X + Y ~ N(0, √(1² + 2²)) = N(0, √5):

Let’s sample from these distributions and visualize them:

Now let’s compute the sum S = X + Y and visualize all three distributions:

X = torch.distributions.Normal(0, 1)
Y = torch.distributions.Normal(0, 2)

x_range = torch.linspace(-5, 5, 1000)
X_pdf = X.log_prob(x_range).exp()
Y_pdf = Y.log_prob(x_range).exp()

plt.figure(figsize=(10, 5))
plt.plot(x_range.numpy(), X_pdf.numpy(), label='X ~ N(0, 1)', color='blue')
plt.plot(x_range.numpy(), Y_pdf.numpy(), label='Y ~ N(0, 2)', color='orange')

plt.title('Probability Density Functions')
plt.legend()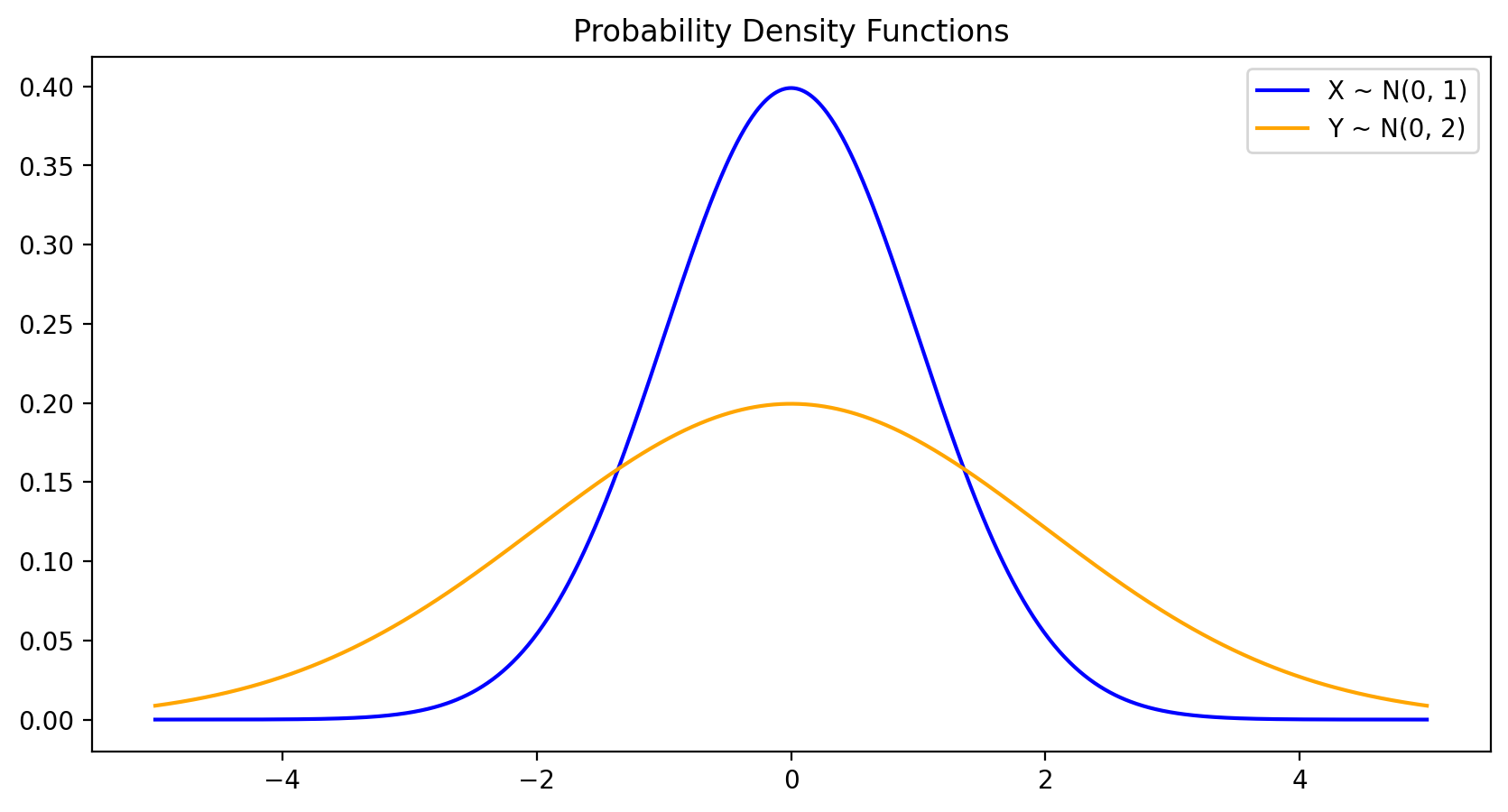

x_samples = X.sample((10000,))
y_samples = Y.sample((10000,))
fig, ax = plt.subplots(2, 1, figsize=(6, 6), sharex=True)
ax[0].hist(x_samples.numpy(), bins=30, density=True, alpha=0.5, color='blue')
ax[1]. hist(y_samples.numpy(), bins=30, density=True, alpha=0.5, color='orange')
ax[0].set_title('X ~ N(0, 1)')
ax[1].set_title('Y ~ N(0, 2)')
plt.xlabel('x')
fig.tight_layout()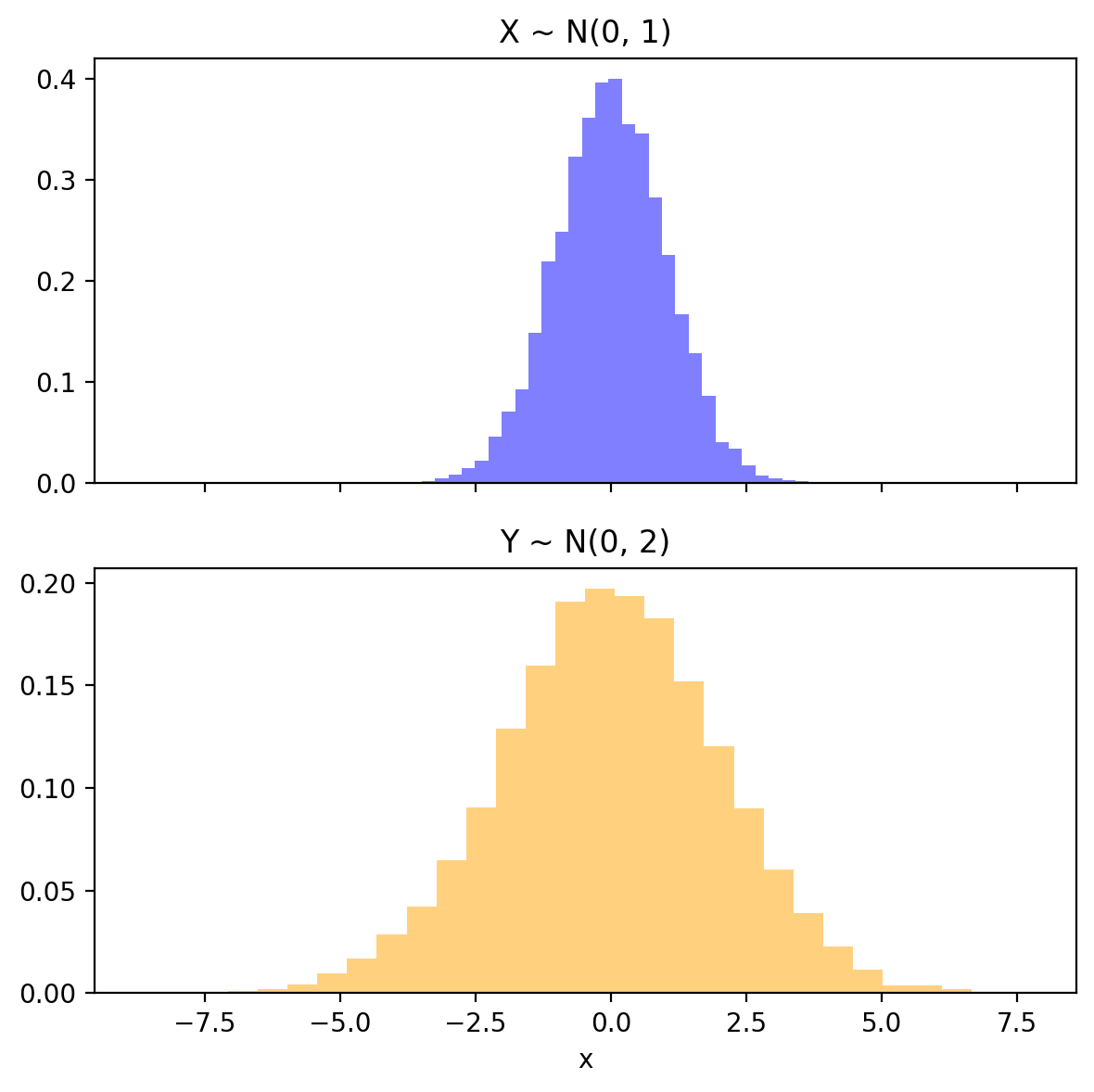

s_samples = x_samples + y_samples
fig, ax = plt.subplots(3, 1, figsize=(6, 9), sharex=True)
ax[0].hist(x_samples.numpy(), bins=30, density=True, alpha=0.5, color='blue')
ax[1].hist(y_samples.numpy(), bins=30, density=True, alpha=0.5, color='orange')
ax[2].hist(s_samples.numpy(), bins=30, density=True, alpha=0.5, color='green')
ax[0].set_title('X ~ N(0, 1)')
ax[1].set_title('Y ~ N(0, 2)')
ax[2].set_title('S = X + Y')
plt.xlabel('x')
plt.tight_layout()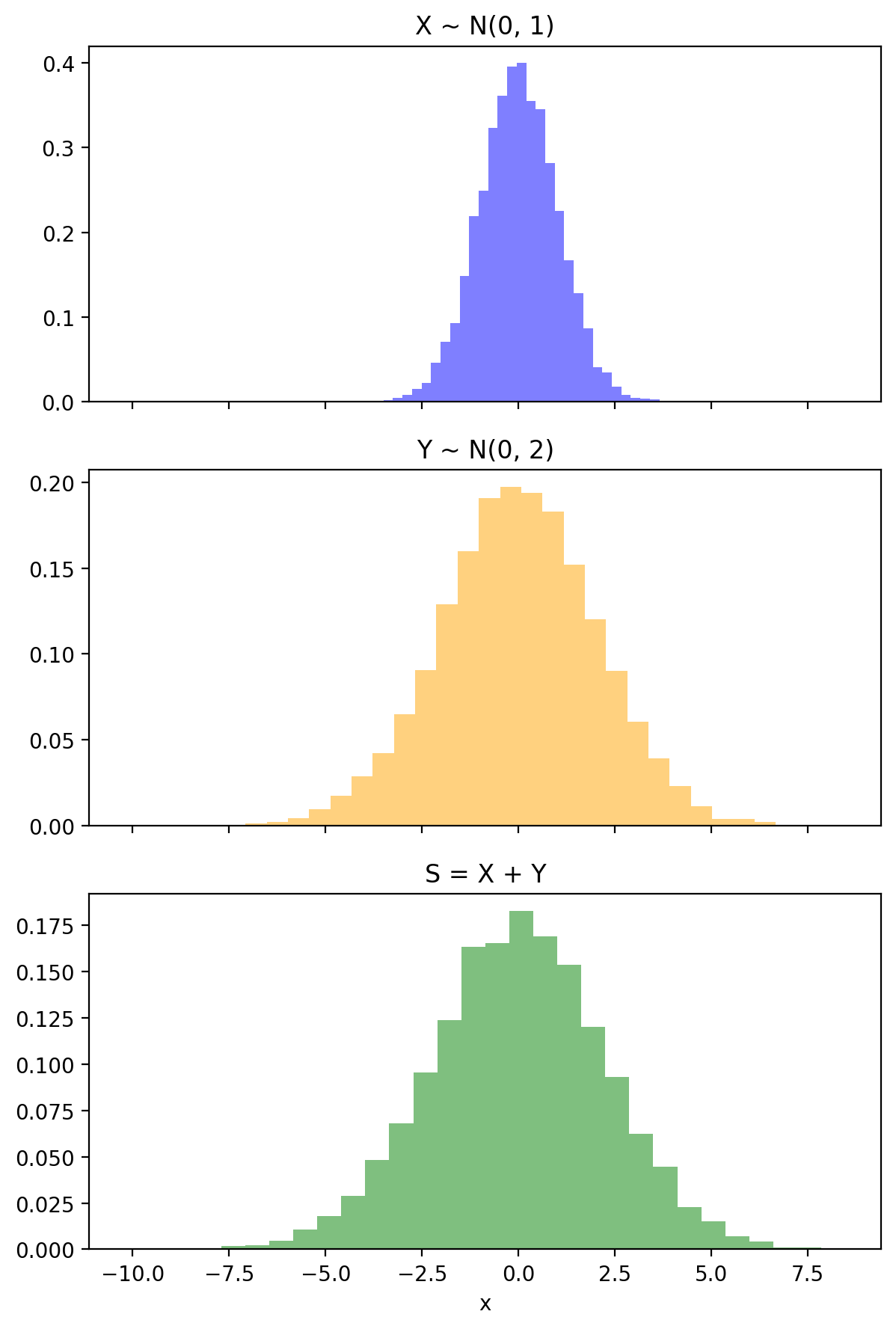

torch.distributions.Normal?

Init signature: torch.distributions.Normal(loc, scale, validate_args=None)

Docstring:     

Creates a normal (also called Gaussian) distribution parameterized by

:attr:`loc` and :attr:`scale`.



Example::



    >>> # xdoctest: +IGNORE_WANT("non-deterministic")

    >>> m = Normal(torch.tensor([0.0]), torch.tensor([1.0]))

    >>> m.sample()  # normally distributed with loc=0 and scale=1

    tensor([ 0.1046])



Args:

    loc (float or Tensor): mean of the distribution (often referred to as mu)

    scale (float or Tensor): standard deviation of the distribution

        (often referred to as sigma)

File:           ~/base/lib/python3.12/site-packages/torch/distributions/normal.py

Type:           type

Subclasses:     

sns.kdeplot(x_samples.numpy(), label='X ~ N(0, 1)', color='blue', bw_adjust=2)
sns.kdeplot(y_samples.numpy(), label='Y ~ N(0, 2)', color='orange', bw_adjust=2)
sns.kdeplot(s_samples.numpy(), label='Z = X + Y', color='green', bw_adjust=2)
plt.title('Kernel Density Estimation')

plt.legend()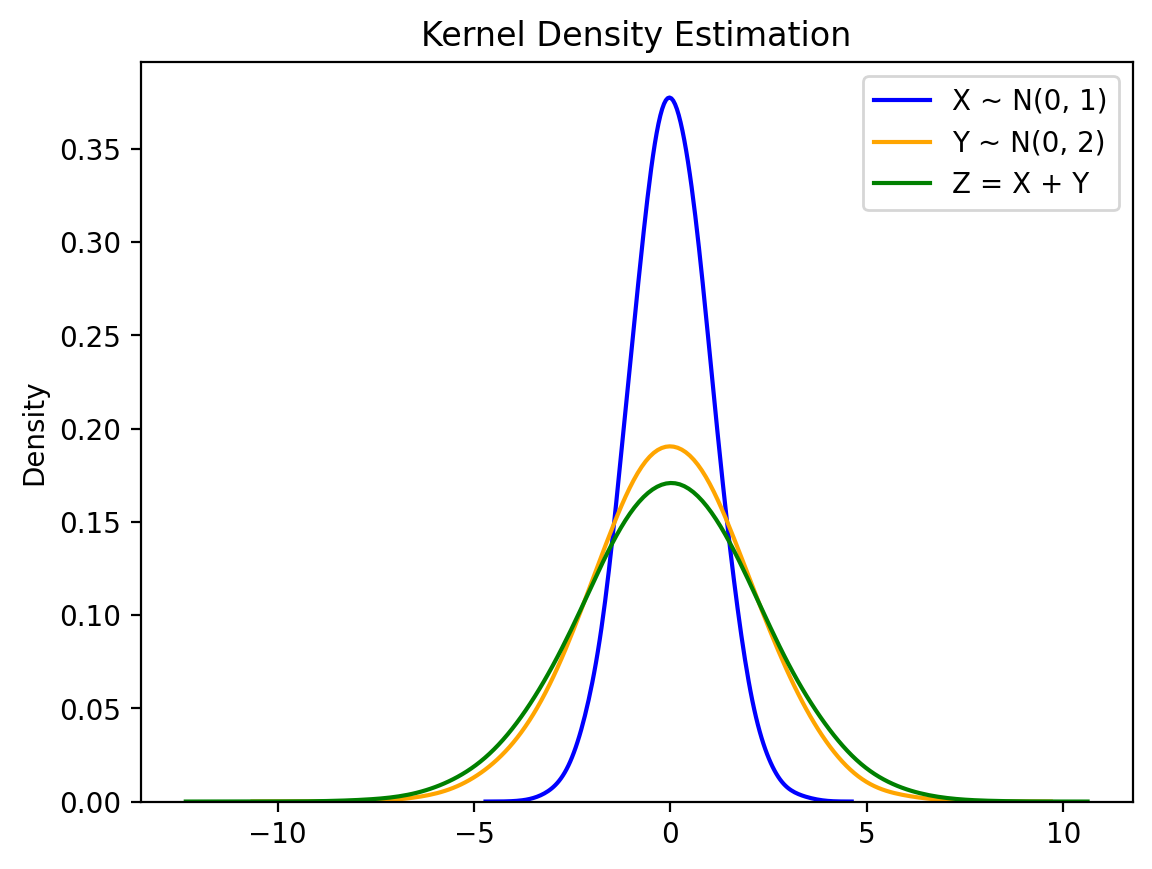

s_samples.std()

tensor(2.2586)

s_samples.mean()

tensor(-0.0113)

s_analytic = torch.distributions.Normal(0, np.sqrt(1**2 + 2**2))
s_analytic.mean, s_analytic.stddev

(tensor(0.), tensor(2.2361))

sns.kdeplot(s_samples.numpy(), label='Z = X + Y', color='green', bw_adjust=2)
s_range = torch.linspace(-10, 10, 1000)
s_pdf = s_analytic.log_prob(s_range).exp()
plt.plot(s_range.numpy(), s_pdf.numpy(), label='Z ~ N(0, sqrt(5))', color='red')
plt.legend()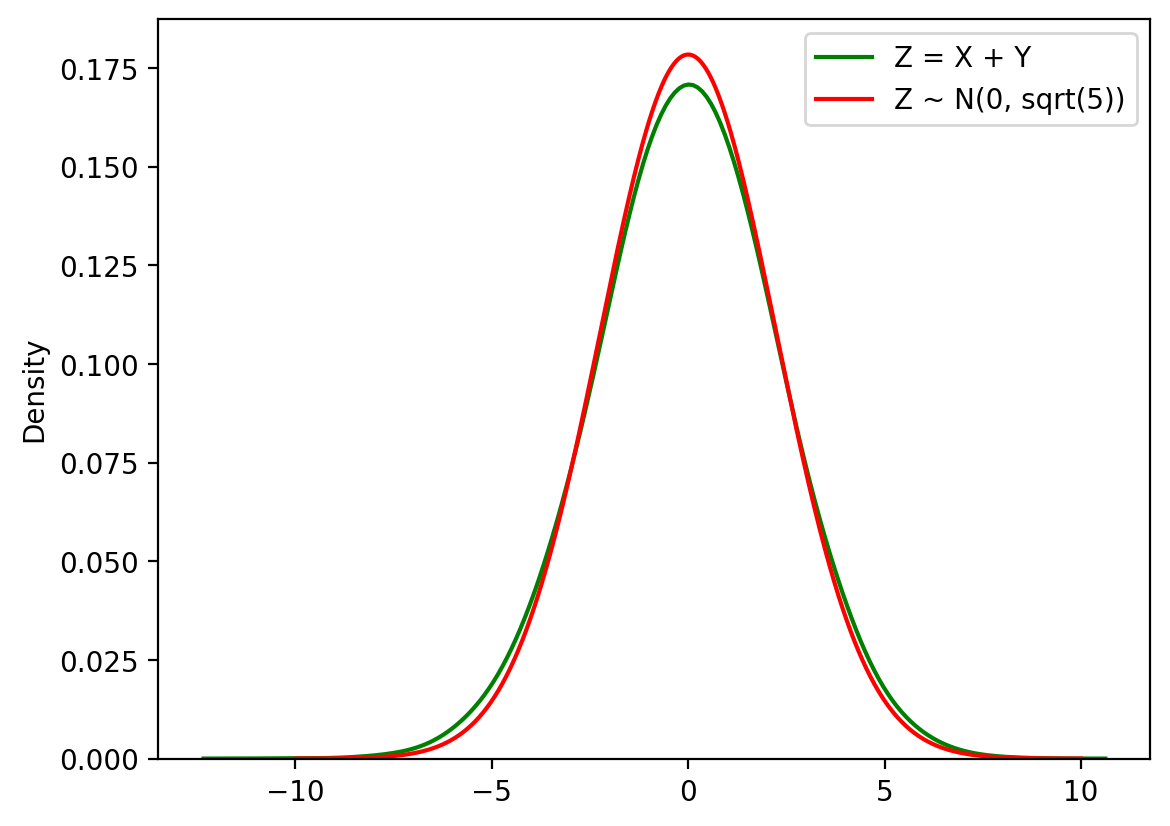

### Example 2

X = torch.distributions.Categorical(torch.tensor([0.25, 0.25, 0.25, 0.25]))
Y = torch.distributions.Categorical(torch.tensor([0.25, 0.25, 0.25, 0.25]))

x_samples = X.sample((10000,))
y_samples = Y.sample((10000,))

fig, ax = plt.subplots(2, 1, figsize=(6, 6), sharex=True)

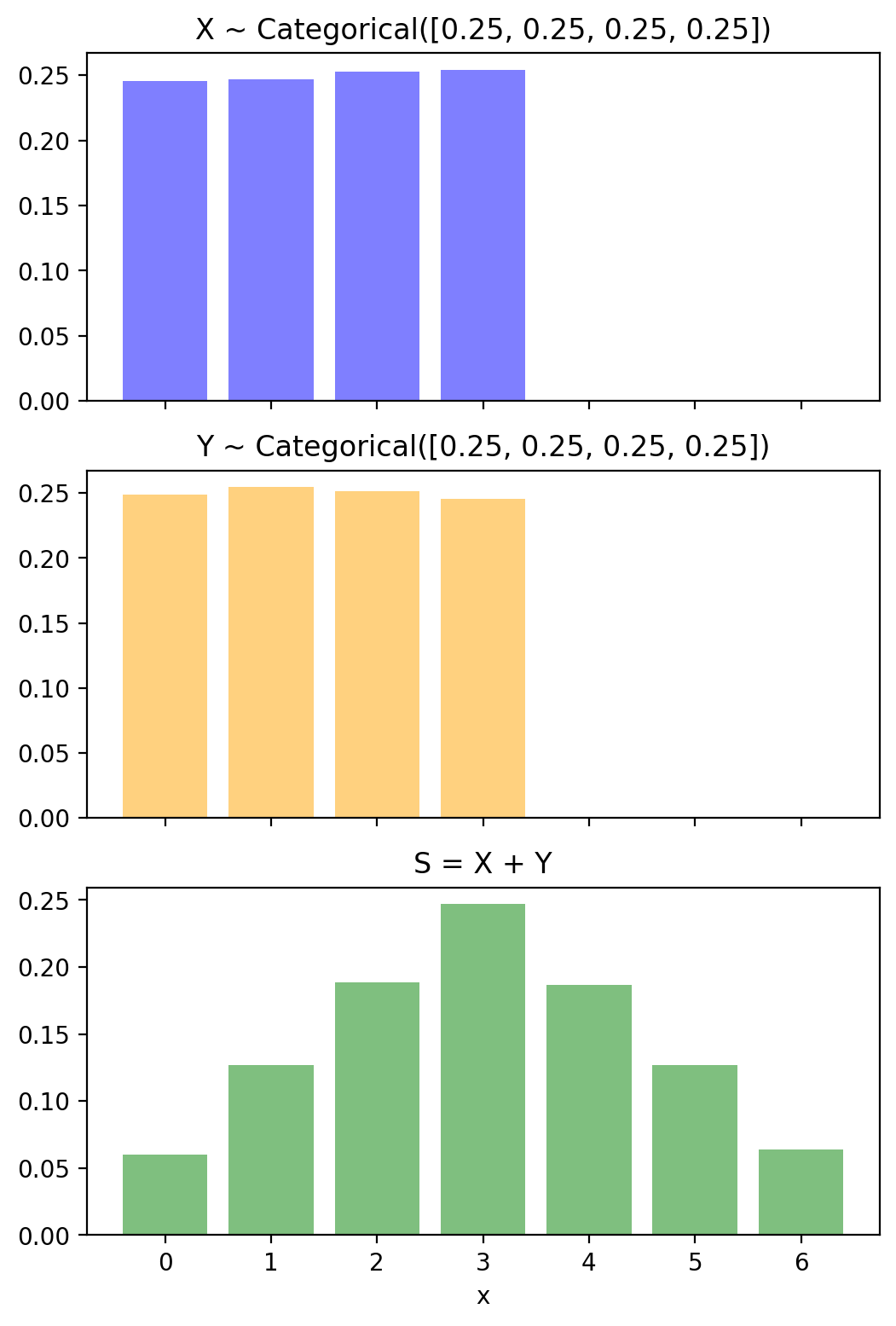
x_samples_normed = pd.Series(x_samples.numpy()).value_counts(normalize=True).sort_index()
y_samples_normed = pd.Series(y_samples.numpy()).value_counts(normalize=True).sort_index()

ax[0].bar(x_samples_normed.index, x_samples_normed.values, alpha=0.5, color='blue')
ax[1].bar(y_samples_normed.index, y_samples_normed.values, alpha=0.5, color='orange')
ax[0].set_title('X ~ Categorical([0.25, 0.25, 0.25, 0.25])')
ax[1].set_title('Y ~ Categorical([0.25, 0.25, 0.25, 0.25])')
plt.xlabel('x')

Text(0.5, 0, 'x')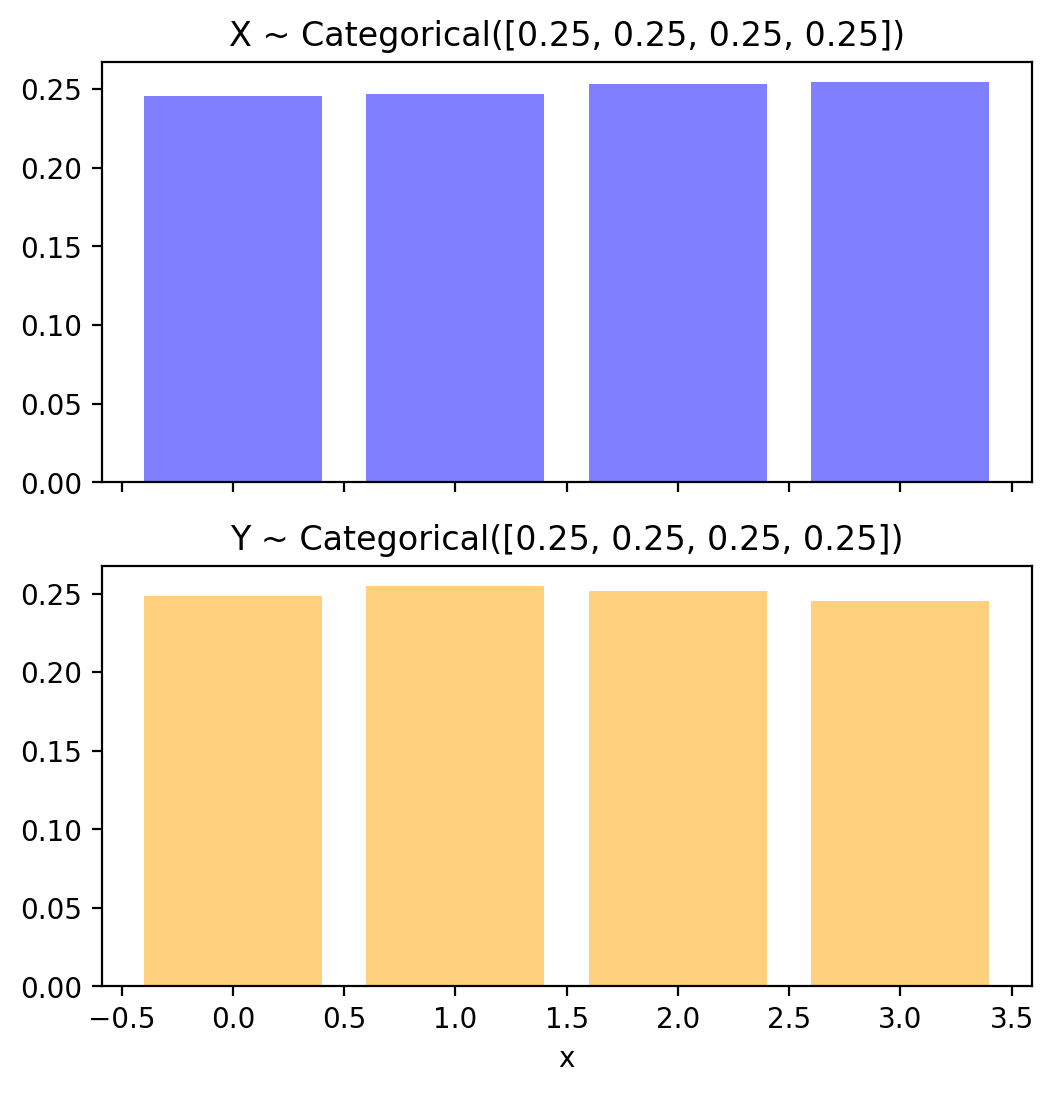

s_samples = x_samples + y_samples
fig, ax = plt.subplots(3, 1, figsize=(6, 9), sharex=True)
s_samples_normed = pd.Series(s_samples.numpy()).value_counts(normalize=True).sort_index()
ax[0].bar(x_samples_normed.index, x_samples_normed.values, alpha=0.5, color='blue')
ax[1].bar(y_samples_normed.index, y_samples_normed.values, alpha=0.5, color='orange')
ax[2].bar(s_samples_normed.index, s_samples_normed.values, alpha=0.5, color='green')
ax[0].set_title('X ~ Categorical([0.25, 0.25, 0.25, 0.25])')
ax[1].set_title('Y ~ Categorical([0.25, 0.25, 0.25, 0.25])')
ax[2].set_title('S = X + Y')
plt.xlabel('x')

Text(0.5, 0, 'x')