Word Embeddings and Vector Angles

Data Science

Machine Learning

Linear Algebra

Mathematics

Understanding vector similarities and angles in word embeddings using cosine similarity and vector operations for natural language processing applications

Author

Nipun Batra

Published

March 23, 2025

Keywords

embeddings, word2vec, cosine similarity, vector angles, natural language processing, similarity measures

import numpy as np
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'

Word Embeddings and Vector Angles

Introduction

This notebook explores the fascinating relationship between vector angles and semantic similarity in word embeddings. We’ll demonstrate how geometric concepts from linear algebra apply to natural language processing, particularly in measuring word similarities.

Learning Objectives

By the end of this notebook, you will understand: - How to calculate angles between vectors using dot products - The concept of cosine similarity in vector spaces - How word embeddings capture semantic relationships - The practical application of vector geometry in NLP

Prerequisites

Basic linear algebra (vectors, dot products)
Understanding of Python and NumPy
Familiarity with the concept of word embeddings

Vector Angles: Mathematical Foundation

We begin with a simple example of computing angles between 2D vectors. The angle between two vectors can be calculated using the dot product formula:

\[\cos(\theta) = \frac{\mathbf{v_1} \cdot \mathbf{v_2}}{|\mathbf{v_1}| \cdot |\mathbf{v_2}|}\]

Where \(\theta\) is the angle between vectors \(\mathbf{v_1}\) and \(\mathbf{v_2}\).

Exploring Different Vector Combinations

Notice how the angle changes as we modify the vectors. Perpendicular vectors have a 90° angle, while parallel vectors have 0° angle.

Word Embeddings: From Words to Vectors

Now we transition to the main topic: word embeddings. Word embeddings are dense vector representations of words that capture semantic relationships. We’ll use pre-trained GloVe embeddings to explore how words relate to each other in vector space.

Loading Pre-trained Word Embeddings

We’ll use the GloVe (Global Vectors for Word Representation) model, which creates word embeddings by analyzing word co-occurrence statistics from large text corpora.

Example 1: Simple 2D Vector Angles

Let’s start with basic examples to understand how angles work with simple vectors.

Examining Word Vectors

Let’s look at the actual vector representation of the word “king”. Each word is represented as a 50-dimensional vector where each dimension captures different semantic features.

def angle_between(v1, v2):
    cos_theta = np.dot(v1, v2) / (np.linalg.norm(v1) * np.linalg.norm(v2))
    return np.arccos(np.clip(cos_theta, -1.0, 1.0)) * 180 / np.pi

v1 = np.array([1, 0])
v2 = np.array([1, 1])

plt.quiver([0, 0], [0, 0], [v1[0], v2[0]], [v1[1], v2[1]], angles='xy', scale_units='xy', scale=1)
plt.xlim(-1, 2)
plt.ylim(-1, 2)

print(f"Angle: {angle_between(v1, v2):.2f}°")

Angle: 45.00°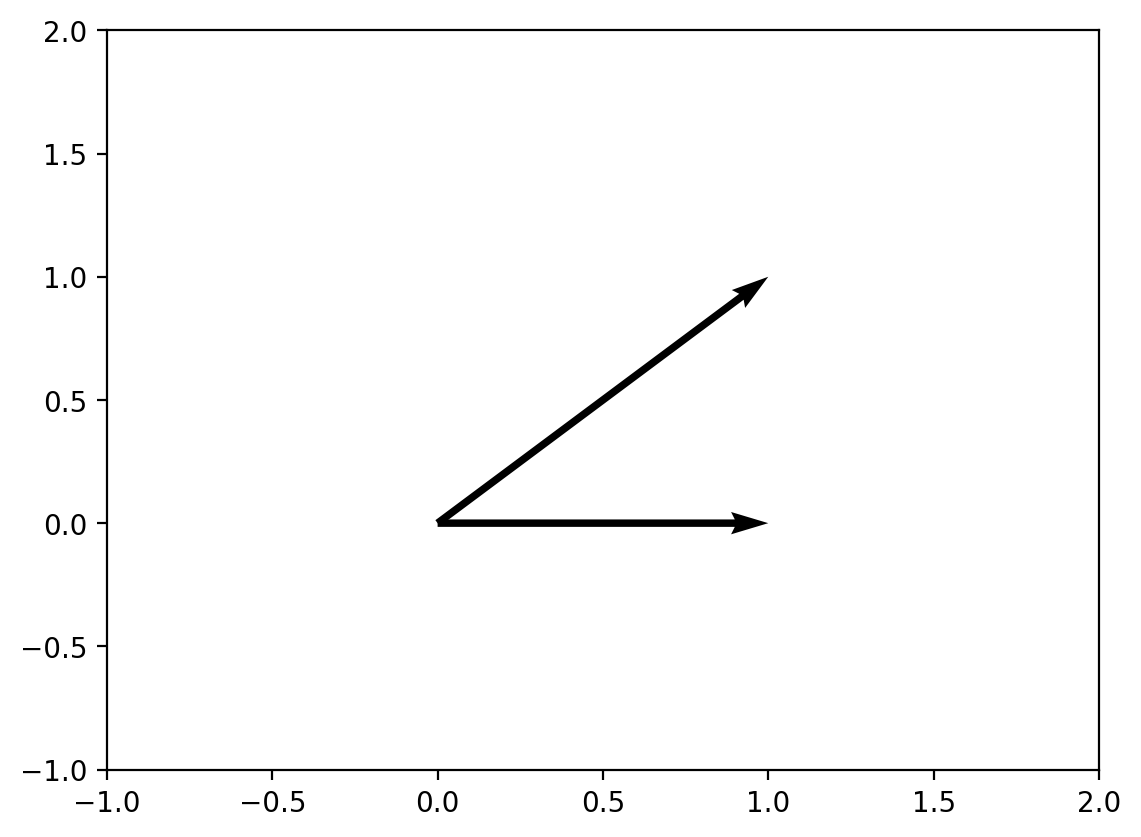

Measuring Semantic Similarity with Angles

King and Queen: A Classic Example

The angle between “king” and “queen” vectors demonstrates how semantically related words have smaller angles between their vector representations. This is a fundamental principle in word embeddings.

Family Relationships in Vector Space

Family relationship words like “uncle” and “aunt” should have relatively small angles since they represent similar family concepts.

Dissimilar Words: Larger Angles

When we compare semantically unrelated words like “king” and “python” (the programming language), we expect to see much larger angles, indicating low semantic similarity.

Exploring Word Neighborhoods

Finding Similar Words

The most_similar function finds words with the smallest angles (highest cosine similarity) to a given word. This demonstrates how vector space geometry captures semantic relationships.

Finding Dissimilar Words

Conversely, we can find words that are most dissimilar (largest angles) to understand what the model considers semantically distant.

Verification: Computing Angles with Dissimilar Words

Let’s verify our findings by computing the actual angle between “king” and one of the most dissimilar words.

Key Insights and Conclusions

What We’ve Learned

Vector Angles and Similarity: Smaller angles between word vectors indicate greater semantic similarity
Cosine Similarity: This metric (cosine of the angle) is widely used in NLP for measuring word similarity
Geometric Intuition: Word embeddings transform linguistic relationships into geometric relationships in high-dimensional space
Practical Applications: These concepts are fundamental to search engines, recommendation systems, and many NLP tasks

Mathematical Relationship

The relationship between angle \(\theta\) and cosine similarity is: - \(\theta = 0°\) → \(\cos(\theta) = 1\) → Perfect similarity - \(\theta = 90°\) → \(\cos(\theta) = 0\) → No correlation
- \(\theta = 180°\) → \(\cos(\theta) = -1\) → Perfect opposition

Real-world Applications

Understanding vector angles in embeddings is crucial for: - Information Retrieval: Finding relevant documents - Recommendation Systems: Suggesting similar items - Machine Translation: Aligning words across languages - Sentiment Analysis: Understanding emotional relationships between words

print(f"Angle: {angle_between(v1, np.array([0, 1])):.2f}°")
plt.quiver([0, 0], [0, 0], [v1[0], 0], [v1[1], 1], angles='xy', scale_units='xy', scale=1)
plt.xlim(-1, 2)
plt.ylim(-1, 2)

Angle: 90.00°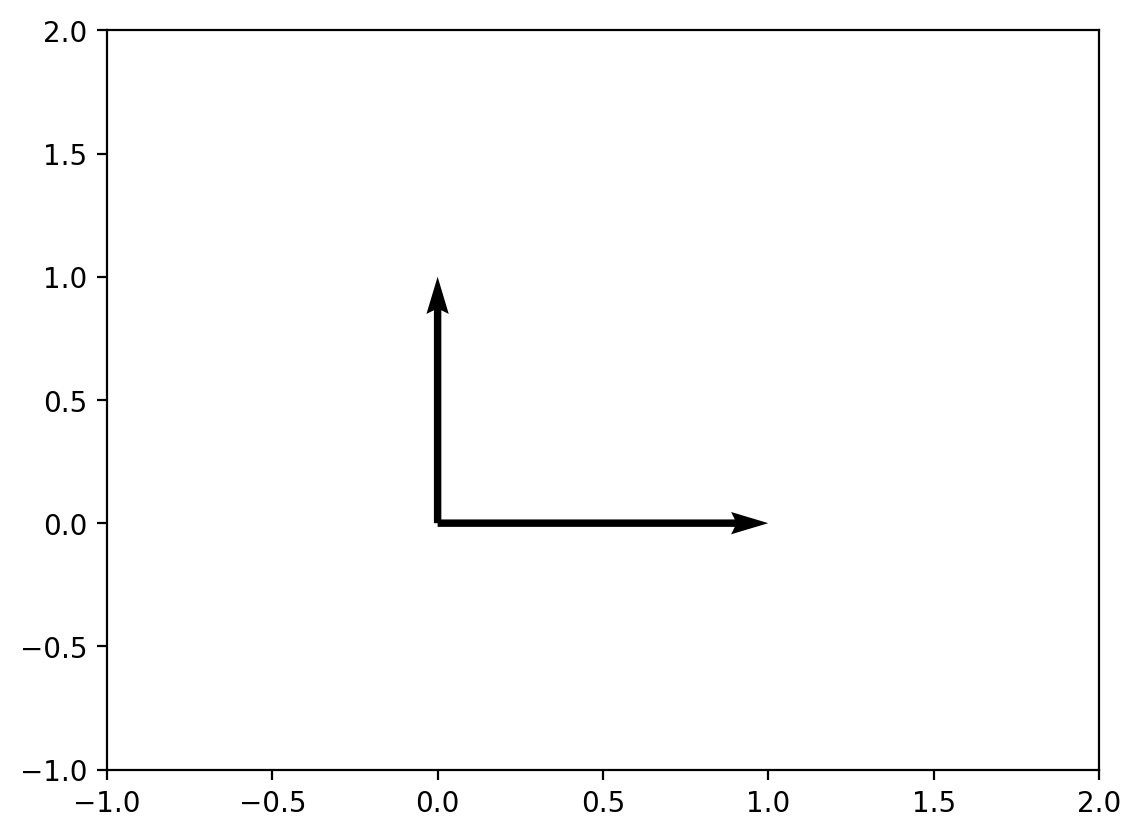

import gensim.downloader as api
from scipy.spatial.distance import cosine

model = api.load("glove-wiki-gigaword-50")  # Small 50D GloVe model

def get_cosine_similarity(word1, word2):
    v1 = model[word1]
    v2 = model[word2]
    return angle_between(v1, v2)

word1 = "king"
v1 = model[word1]

v1

array([ 0.50451 ,  0.68607 , -0.59517 , -0.022801,  0.60046 , -0.13498 ,
       -0.08813 ,  0.47377 , -0.61798 , -0.31012 , -0.076666,  1.493   ,
       -0.034189, -0.98173 ,  0.68229 ,  0.81722 , -0.51874 , -0.31503 ,
       -0.55809 ,  0.66421 ,  0.1961  , -0.13495 , -0.11476 , -0.30344 ,
        0.41177 , -2.223   , -1.0756  , -1.0783  , -0.34354 ,  0.33505 ,
        1.9927  , -0.04234 , -0.64319 ,  0.71125 ,  0.49159 ,  0.16754 ,
        0.34344 , -0.25663 , -0.8523  ,  0.1661  ,  0.40102 ,  1.1685  ,
       -1.0137  , -0.21585 , -0.15155 ,  0.78321 , -0.91241 , -1.6106  ,
       -0.64426 , -0.51042 ], dtype=float32)

word2 = "queen"
v2 = model[word2]
print(v2)

[ 0.37854    1.8233    -1.2648    -0.1043     0.35829    0.60029
 -0.17538    0.83767   -0.056798  -0.75795    0.22681    0.98587
  0.60587   -0.31419    0.28877    0.56013   -0.77456    0.071421
 -0.5741     0.21342    0.57674    0.3868    -0.12574    0.28012
  0.28135   -1.8053    -1.0421    -0.19255   -0.55375   -0.054526
  1.5574     0.39296   -0.2475     0.34251    0.45365    0.16237
  0.52464   -0.070272  -0.83744   -1.0326     0.45946    0.25302
 -0.17837   -0.73398   -0.20025    0.2347    -0.56095   -2.2839
  0.0092753 -0.60284  ]

angle_between(v1, v2)

38.3805515334704

angle_between(model["uncle"], model["aunt"])

40.26145236751397

# Now some dissimilar words
angle_between(model["king"], model["python"])

79.36413285046953

model.most_similar("king")

[('prince', 0.8236179351806641),
 ('queen', 0.7839044332504272),
 ('ii', 0.7746230363845825),
 ('emperor', 0.7736247777938843),
 ('son', 0.766719400882721),
 ('uncle', 0.7627150416374207),
 ('kingdom', 0.7542160749435425),
 ('throne', 0.7539914846420288),
 ('brother', 0.7492411136627197),
 ('ruler', 0.7434254288673401)]

# most dissimilar words to "king"
model.most_similar(negative=["king"])

[('4,835', 0.729358434677124),
 ('rules-based', 0.7123876810073853),
 ('renos', 0.7085371613502502),
 ('meawhile', 0.706490159034729),
 ('nanobiotechnology', 0.6925080418586731),
 ('m-42', 0.6916395425796509),
 ('poligny', 0.6882078051567078),
 ('onyekwe', 0.6877189874649048),
 ('asie', 0.6861312985420227),
 ('metabolomics', 0.682388961315155)]

angle_between(model["king"], model["rules-based"])

135.42952204160463